Question

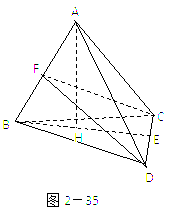如图2－35：在空间四边形ABCD中，已知BC＝AC，AD＝BD，引BE⊥CD，E为垂足，作AH⊥BE于H，求证：AH⊥平面BCD。

Answer 1

解析:

要证AH⊥平面BCD，只须利用直线和平面垂直的判定定理，证AH垂直于平面BCD中两条相交直线即可。

证明:取AB中点F，连结CF、DF，

∵AC＝BC，∴CF⊥AB，

又∵AD＝BD，∴DF⊥AB，∴AB⊥平面CDF，

又CD平面CDF，∴CD⊥AB

又CD⊥BE，∴CD⊥平面ABE，CD⊥AH

又AH⊥BE，∴AH⊥平面BCD。

点评:证明线面垂直，需转化为线线垂直，而线线垂直，又可通过证线面垂直来实现。在这里，定义可以双向使用，即直线a垂直于平面α内的任何直线，则a⊥α，反之，若a⊥α，则a垂直于平面α内的任何直线。