题目内容
已知函数f（x）=2x+alnx．
（1）若a＜0证明：对于任意的两个正数x1，x2，总有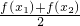
≥f（
）成立；
（2）若对任意的x∈[1，e]，不等式：f（x）≤（a+3）x-
x2恒成立，求a的取值范围．
解：（1）由：
，
而：
，
又因为：a＜0，所以：
，即：
成立．
（2）由
恒成立，即只要：
成立；
又x∈[1，e]，易知x-lnx＞0
令
（x∈[1，e]）
，
令：
，
h（x）min=h（2）=2-ln2＞0，∴g′（x）＞0
所以：g（x）在x∈[1，e]上为增函数．
即：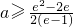
分析：（1）将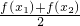与f（）进行作差与0进行比较，利用均值不等式以及对数函数的性质可判定符号；
（2）由恒成立，转化成只要：成立，根据自变量的范围将a分离出来，利用导数研究不等式另一侧函数在闭区间上的最小值即可．
点评：本题主要考查了函数恒成立问题，以及利用导数研究函数最值，属于基础题．
，而：
，又因为：a＜0，所以：
，即：成立．（2）由
恒成立，即只要：成立；又x∈[1，e]，易知x-lnx＞0
令
（x∈[1，e]），令：
，h（x）min=h（2）=2-ln2＞0，∴g′（x）＞0所以：g（x）在x∈[1，e]上为增函数．
即：
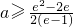
分析：（1）将
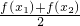与f（）进行作差与0进行比较，利用均值不等式以及对数函数的性质可判定符号；（2）由
恒成立，转化成只要：成立，根据自变量的范围将a分离出来，利用导数研究不等式另一侧函数在闭区间上的最小值即可．点评：本题主要考查了函数恒成立问题，以及利用导数研究函数最值，属于基础题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目