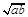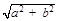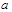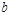题目内容
已知双曲线 的右焦点为F,P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于
的右焦点为F,P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于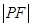 ,则
,则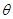 的值为( )
的值为( )
A.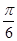 | B.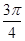 | C.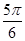 | D.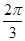 |
C
解析由a2=cos2θ,b2=sin2θ, ,知a=﹣cosθ,b=sinθ,c=1,e=﹣
,知a=﹣cosθ,b=sinθ,c=1,e=﹣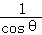 ,再由双曲线第二定义,知
,再由双曲线第二定义,知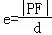 ,d=
,d=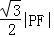 ,故e=﹣
,故e=﹣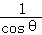 =
=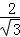 ,由此能够导出θ的值.
,由此能够导出θ的值.
∵a2=cos2θ,b2=sin2θ, ,
,
∴a=﹣cosθ,b=sinθ,c=1,e=﹣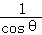 ,
,
由双曲线第二定义,知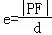 ,
,
d=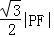 ,
,
∴e=﹣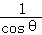 =
=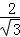 ,
,
∴cosθ=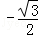 ,
,
∵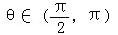 ,∴
,∴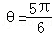 .
.
故选C.

练习册系列答案
相关题目
已知双曲线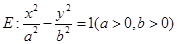 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为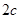 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 ( )
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 ( )
| A. | B.3 | C. | D. |
双曲线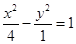 的渐近线方程是
的渐近线方程是
A.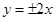 | B.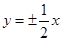 | C.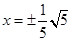 | D.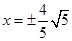 |
已知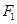 、
、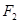 为双曲线C:
为双曲线C: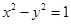 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠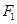
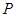
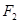 =
=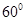 ,则
,则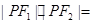 ( *** )
( *** )
| A.2 | B.4 | C.6 | D.8 |
椭圆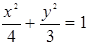 的右焦点到直线
的右焦点到直线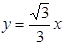 的距离是( )
的距离是( )
A.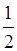 | B.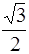 | C.1 | D.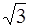 |
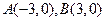 的距离之差的绝对值等于6的点M的轨迹为 ( ■ )
的距离之差的绝对值等于6的点M的轨迹为 ( ■ ) . 两条射线
. 两条射线
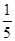
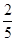
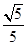
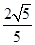
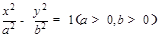 ,以C的右焦点为圆心且与C的渐近线相切的圆的半径是( )
,以C的右焦点为圆心且与C的渐近线相切的圆的半径是( )