题目内容
设非零实常数a、b、c满足a、b同号,b、c异号,则关于x的方程a.4x+b.2x+c=0( )A.无实根
B.有两个共轭的虚根
C.有两个异号的实根
D.仅有一个实根
【答案】分析:先设2x=t,则原方程可化为:at2+bt+c=0,根据a、b、c满足a、b同号,b、c异号,研究其根的分布情况,得到方程at2+bt+c=0的两根是一正一负,由于2x=t,从而得出关于x的方程a.4x+b.2x+c=0根的情况.
解答:解:设2x=t,则原方程可化为:
at2+bt+c=0,由于a、b、c满足a、b同号,b、c异号,
其△=b2-4ac>0,且两根之和- ,两根之积
,两根之积 ,
,
故方程at2+bt+c=0的两根是一正一负,
由于2x=t,则关于x的方程a.4x+b.2x+c=0仅有一个实根,
故选D.
点评:本小题主要考查函数与方程的综合运用、方程的解法、根的分布等基础知识,考查运算求解能力、换元思想.属于基础题.
解答:解:设2x=t,则原方程可化为:
at2+bt+c=0,由于a、b、c满足a、b同号,b、c异号,
其△=b2-4ac>0,且两根之和-
 ,两根之积
,两根之积 ,
,故方程at2+bt+c=0的两根是一正一负,
由于2x=t,则关于x的方程a.4x+b.2x+c=0仅有一个实根,
故选D.
点评:本小题主要考查函数与方程的综合运用、方程的解法、根的分布等基础知识,考查运算求解能力、换元思想.属于基础题.

练习册系列答案
相关题目
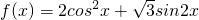 ,
,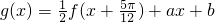 ,其中a,b为非零实常数.
,其中a,b为非零实常数.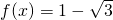 ,
,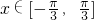 ,求x;
,求x;