题目内容
 如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
如图,已知正方体ABCD-A1B1C1D1,棱长为4,E为面A1D1DA的中心,
CF=3FC1,AH=3HD,
(1)求异面直线EB1与HF之间的距离
(2)求二面角H-B1E-A1的平面角的余弦值.
解:如图建立直角坐标系D1-xyz,则E(2,0,2),B1(4,4,0),H(1,0,4)
(1)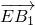 =(2,4,-2),
=(2,4,-2), =(-1,4,-3)
=(-1,4,-3) =(-1,0,2),设
=(-1,0,2),设 =(x,y,z)
=(x,y,z)
 即
即
,取x=1,则z=-3,y=-2,
则 =(1,-2,-3)
=(1,-2,-3)
异面直线EB1与HF之间的距离为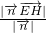 =
=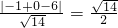
(2))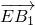 =(2,4,-2),
=(2,4,-2),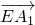 =(2,0,-2),
=(2,0,-2), =(-1,0,2),
=(-1,0,2),
设平面HB1E的法向量为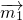 =(x,y,z)
=(x,y,z)
则 即
即
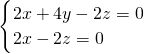 取x=2,则y=
取x=2,则y= ,z=1.∴
,z=1.∴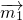 =(2,
=(2, ,1)
,1)
令平面A1B1E的法向量为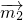 =(x,y,z)
=(x,y,z)
则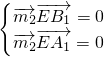
取x=1,y=0,z=1,则为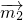 =(1,0,1)
=(1,0,1)
∴|cos |=
|=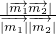 =
= .
.
∵二面角H-B1E-A为钝二面角.
∴二面角H-B1E-A1的平面角的余弦值为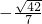 .
.
分析:(1)求出异面直线EB1与HF的方向向量,以及与它们垂直的向量 ,异面直线EB1与HF之间的距离等于
,异面直线EB1与HF之间的距离等于 .
.
(2)求出平面HB1E的法向量为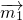 ,平面A1B1E的法向量为
,平面A1B1E的法向量为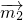 ,二面角H-B1E-A1的平面角的余弦值的绝对值等于
,二面角H-B1E-A1的平面角的余弦值的绝对值等于 夹角的余弦绝对值.
夹角的余弦绝对值.
点评:本题考查异面直线距离,二面角的大小计算.做题的关键是熟练掌握向量法求异面直线距离、二面角的公式与步骤,利用向量法求空间距离、空间角是向量的一个重要运用,向量的引入,为立体几何中二面角求解带来了极大的方便,题后应注意总结此法求二面角的规律.
(1)
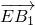 =(2,4,-2),
=(2,4,-2), =(-1,4,-3)
=(-1,4,-3) =(-1,0,2),设
=(-1,0,2),设 =(x,y,z)
=(x,y,z) 即
即
,取x=1,则z=-3,y=-2,
则
 =(1,-2,-3)
=(1,-2,-3)异面直线EB1与HF之间的距离为
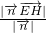 =
=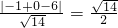
(2))
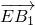 =(2,4,-2),
=(2,4,-2),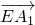 =(2,0,-2),
=(2,0,-2), =(-1,0,2),
=(-1,0,2),设平面HB1E的法向量为
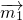 =(x,y,z)
=(x,y,z)则
 即
即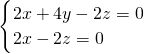 取x=2,则y=
取x=2,则y= ,z=1.∴
,z=1.∴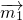 =(2,
=(2, ,1)
,1)令平面A1B1E的法向量为
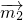 =(x,y,z)
=(x,y,z)则
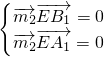
取x=1,y=0,z=1,则为
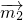 =(1,0,1)
=(1,0,1)∴|cos
 |=
|=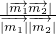 =
= .
.∵二面角H-B1E-A为钝二面角.
∴二面角H-B1E-A1的平面角的余弦值为
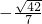 .
.分析:(1)求出异面直线EB1与HF的方向向量,以及与它们垂直的向量
 ,异面直线EB1与HF之间的距离等于
,异面直线EB1与HF之间的距离等于 .
.(2)求出平面HB1E的法向量为
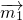 ,平面A1B1E的法向量为
,平面A1B1E的法向量为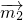 ,二面角H-B1E-A1的平面角的余弦值的绝对值等于
,二面角H-B1E-A1的平面角的余弦值的绝对值等于 夹角的余弦绝对值.
夹角的余弦绝对值.点评:本题考查异面直线距离,二面角的大小计算.做题的关键是熟练掌握向量法求异面直线距离、二面角的公式与步骤,利用向量法求空间距离、空间角是向量的一个重要运用,向量的引入,为立体几何中二面角求解带来了极大的方便,题后应注意总结此法求二面角的规律.

练习册系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )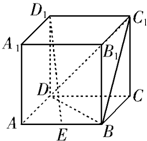 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.