题目内容
“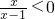 成立”是“x(x-3)<0成立”的
成立”是“x(x-3)<0成立”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:先分别解不等式,利用集合之间的关系,根据必要条件、充分条件与充要条件的定义加以判断.
解答:由题意,“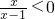 成立”,即0<x<1;
成立”,即0<x<1;
“x(x-3)<0成立”,即0<x<3;
由于0<x<1时,一定有0<x<3,反之不成立
故“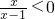 成立”是“x(x-3)<0成立”的充分不必要条件
成立”是“x(x-3)<0成立”的充分不必要条件
故选A.
点评:本题的考点是必要条件、充分条件与充要条件的判断,主要考查利用定义判断必要条件、充分条件与充要条件,关键是正确解不等式,从而得出集合之间的关系.
分析:先分别解不等式,利用集合之间的关系,根据必要条件、充分条件与充要条件的定义加以判断.
解答:由题意,“
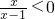 成立”,即0<x<1;
成立”,即0<x<1;“x(x-3)<0成立”,即0<x<3;
由于0<x<1时,一定有0<x<3,反之不成立
故“
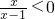 成立”是“x(x-3)<0成立”的充分不必要条件
成立”是“x(x-3)<0成立”的充分不必要条件故选A.
点评:本题的考点是必要条件、充分条件与充要条件的判断,主要考查利用定义判断必要条件、充分条件与充要条件,关键是正确解不等式,从而得出集合之间的关系.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.