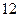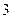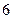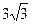题目内容

(1)
 ABCD为直角梯形,AD =
ABCD为直角梯形,AD =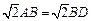 ,
, AB⊥BD,(1分)
AB⊥BD,(1分)PB⊥BD ,AB
 PB =B,AB,PB
PB =B,AB,PB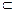 平面PAB,BD⊥平面PAB,( 4分)
平面PAB,BD⊥平面PAB,( 4分)PA
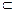 面PAB,
面PAB,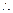 PA ⊥BD.(5分)
PA ⊥BD.(5分) (2)假设PA=PD,取AD 中点N,连PN,BN,则PN⊥AD,BN⊥AD, (7分)
AD⊥平面PNB,得 PB⊥AD,(8分)
又PB⊥BD ,得PB⊥平面ABCD,
∴
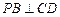 (9分)
(9分)又∵
 ,∴CD⊥平面PBC,
,∴CD⊥平面PBC,∴CD⊥PC, 与已知条件
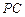 与
与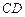
不垂直矛盾
∴
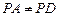 (10分)
(10分)(3)在上l取一点E,使PE=BC,(11分)
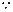 PE∥BC,
PE∥BC,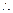 四边形BCPE是平行四边形,(12分)
四边形BCPE是平行四边形,(12分)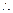 PC∥BE,PC
PC∥BE,PC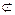 平面EBD, BE
平面EBD, BE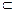 平面EBD
平面EBD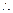 PC∥平面EBD.(14分)
PC∥平面EBD.(14分)略

练习册系列答案
相关题目
 中,高
中,高 是4米,底面的边长是6米。
是4米,底面的边长是6米。
 中,
中, ,
, 是
是 边上任意一点(
边上任意一点( 不重合),若
不重合),若 ,则
,则 =( )
=( )



 中,
中,
 与
与 相交于
相交于 点.若
点.若 则
则 ( )
( )



 中,满足条件
中,满足条件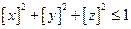 的点
的点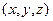 构成的空间区域
构成的空间区域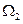 的体积为
的体积为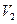 (
(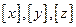 分别表示不大于
分别表示不大于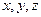 的最大整数),则
的最大整数),则 ,则 ( )
,则 ( )  0
0  0
0 0
0  0
0 的三个顶点为A
的三个顶点为A 、B
、B 、C
、C ,则
,则 的值为 .
的值为 .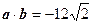 ,
,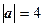 ,
,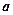 和
和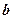 的夹角为
的夹角为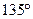 ,则
,则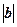 为 ( )
为 ( )