题目内容
(本大题14分)
已知函数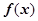 定义域为
定义域为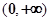 ,且满足
,且满足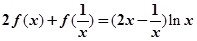 .
.
(Ⅰ)求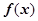 解析式及最小值;
解析式及最小值;
(Ⅱ)求证: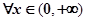 ,
,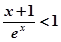 。
。
(Ⅲ)设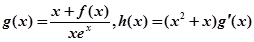 。求证:
。求证: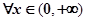 ,
,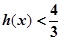 .
.
已知函数
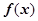 定义域为
定义域为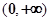 ,且满足
,且满足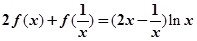 .
.(Ⅰ)求
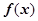 解析式及最小值;
解析式及最小值;(Ⅱ)求证:
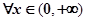 ,
,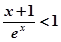 。
。 (Ⅲ)设
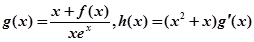 。求证:
。求证: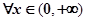 ,
,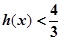 .
.(1) ,
,
(2)见解析;(3)
 ,
,
(2)见解析;(3)

本试题主要是考查了导数在研究函数中的运用。
(1)求解导数,然后判定单调性,然后分析最值。
(2)求解导数可知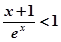
(3)构造函数 ,利用导数分析最值,进而证明不等式。
,利用导数分析最值,进而证明不等式。
解:(1) ,
,
(2)求导可知: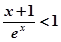
(3) ,
,
故 ,令
,令
求导易知 最大值为
最大值为 ,而
,而 ,且
,且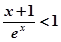
故
(1)求解导数,然后判定单调性,然后分析最值。
(2)求解导数可知
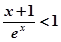
(3)构造函数
 ,利用导数分析最值,进而证明不等式。
,利用导数分析最值,进而证明不等式。解:(1)
 ,
,
(2)求导可知:
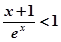
(3)
 ,
,
故
 ,令
,令
求导易知
 最大值为
最大值为 ,而
,而 ,且
,且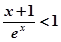
故


练习册系列答案
相关题目
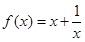 的单调递减区间是
的单调递减区间是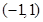
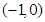
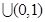
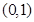
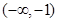 ,
,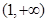
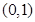 的函数
的函数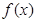 ,对于任意
,对于任意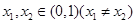 ,恒有
,恒有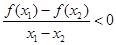 . 若A、B为锐角三角形ABC的两内角,则有( )
. 若A、B为锐角三角形ABC的两内角,则有( )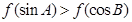 B、
B、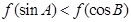
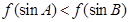 D、
D、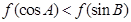
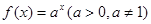 在
在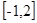 上的最大值为4,最小值为
上的最大值为4,最小值为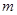 ,且函数
,且函数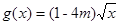 在
在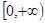 上是增函数,则
上是增函数,则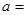 。
。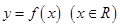 满足
满足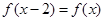 ,且
,且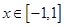 时,
时,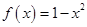
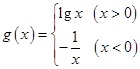 ,则函数
,则函数 在区间
在区间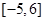 内的零点的个数为
内的零点的个数为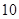
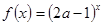 满足
满足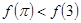 ,则实数
,则实数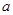 的取值范围是____.
的取值范围是____.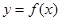 ,存在区间
,存在区间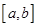 ,当
,当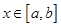 时,
时,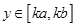
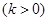 ,则称
,则称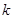 倍值函数。已知
倍值函数。已知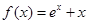 是
是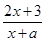 在(-1,+∞)上满足对任意x1<x2,都有f(x1)>f(x2) ,则实数a的取值范围是 .
在(-1,+∞)上满足对任意x1<x2,都有f(x1)>f(x2) ,则实数a的取值范围是 .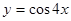 是( )
是( )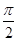 的奇函数
的奇函数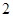
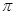 的奇函数
的奇函数