题目内容
设函数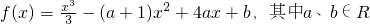 若函数f(x)在x=3处取得极小值是
若函数f(x)在x=3处取得极小值是 ,
,
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的单调递增区间.
解:(I)∵f′(x)=x2-2(a+1)x+4a,
∴f′(3)=9-6(a+1)+4a=0,解得 ,
,
又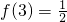 ,
,
所以 -(a+1)•32+4a×3+b=
-(a+1)•32+4a×3+b= ,把a=
,把a= 代入该式,解得b=-4,
代入该式,解得b=-4,
所以a= ,b=-4.
,b=-4.
(Ⅱ)由(Ⅰ)知,f′(x)=x2-5x+6,
由f′(x)>0,得x>3或x<2,
所以函数f(x)的单调递增区间是(-∞,2),(3,+∞).
分析:(Ⅰ)由函数f(x)在x=3处取得极小值是 ,得f′(3)=0,可解得a值,再由f(3)=
,得f′(3)=0,可解得a值,再由f(3)= 可求得b值;
可求得b值;
(Ⅱ)由(Ⅰ)可得f′(x)的表达式,解不等式f′(x)>0即可得到单调增区间;
点评:本题考查利用导数研究函数的极值及单调性问题,属基础题,准确求导,正确理解导数与单调性、极值的关系是解决问题的基础.
∴f′(3)=9-6(a+1)+4a=0,解得
 ,
,又
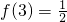 ,
,所以
 -(a+1)•32+4a×3+b=
-(a+1)•32+4a×3+b= ,把a=
,把a= 代入该式,解得b=-4,
代入该式,解得b=-4,所以a=
 ,b=-4.
,b=-4.(Ⅱ)由(Ⅰ)知,f′(x)=x2-5x+6,
由f′(x)>0,得x>3或x<2,
所以函数f(x)的单调递增区间是(-∞,2),(3,+∞).
分析:(Ⅰ)由函数f(x)在x=3处取得极小值是
 ,得f′(3)=0,可解得a值,再由f(3)=
,得f′(3)=0,可解得a值,再由f(3)= 可求得b值;
可求得b值;(Ⅱ)由(Ⅰ)可得f′(x)的表达式,解不等式f′(x)>0即可得到单调增区间;
点评:本题考查利用导数研究函数的极值及单调性问题,属基础题,准确求导,正确理解导数与单调性、极值的关系是解决问题的基础.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目