题目内容
设命题p：函数f（x）=x2-（2a+1）x+6-3a在（-∞，0）上是减函数；命题q：关于x的方程x2+2ax-a=0有实数根．若命题p是真命题，命题q是假命题，求实数a的取值范围．
解：命题p：函数f（x）=x2-（2a+1）x+6-3a在（-∞，0）上是减函数，∴2a+1≥0，∴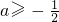
命题q：关于x的方程x2+2ax-a=0有实数根，∴△=4a2+4a≥0，∴a≤-1或a≥0
∴命题非q：-1＜a＜0
因为命题p是真命题，命题q是假命题，
所以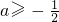且-1＜a＜0
所以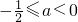
分析：求出命题p、q为真时，a的范围，再利用命题p是真命题，命题q是假命题，即可确定a的取值范围．
点评：本题考查命题真假的运用，解题的关键是求出命题p、q为真时，a的范围，属于中档题．
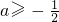
命题q：关于x的方程x2+2ax-a=0有实数根，∴△=4a2+4a≥0，∴a≤-1或a≥0
∴命题非q：-1＜a＜0
因为命题p是真命题，命题q是假命题，
所以
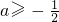且-1＜a＜0所以
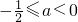
分析：求出命题p、q为真时，a的范围，再利用命题p是真命题，命题q是假命题，即可确定a的取值范围．
点评：本题考查命题真假的运用，解题的关键是求出命题p、q为真时，a的范围，属于中档题．
练习册系列答案
相关题目