Question

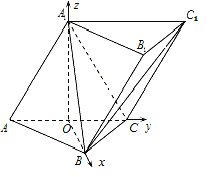
【题目】如图，在三棱柱中，和均是边长为2的等边三角形，点为中点，平面平面.

（1）证明：平面；

（2）求直线与平面所成角的正弦值.

Answer 1

【答案】（1）见解析（2）

【解析】分析：(1)先根据等腰三角形性质得A1O⊥AC，再根据面面垂直性质定理即得结论，（2）先根据条件建立空间直角坐标系，设立各点坐标，利用方程组解得平面A1BC1的法向量，根据向量数量积得向量夹角，最后根据线面角与向量夹角互余关系求结果.

详解：

（Ⅰ）证明：∵AA1=A1C，且O为AC的中点，

∴A1O⊥AC，

又∵平面AA1C1C⊥平面ABC，且交线为AC，又A1O平面AA1C1C，

∴A1O⊥平面ABC

（Ⅱ）如图，以为原点，所在直线为轴，轴，轴建立空间直角坐标系．

由已知可得，, ，

∴，，，

设平面A1BC1的法向量为 ，

则有，

所以的一组解为

设直线与平面所成角为，

则

又∵img src="https://thumb.zyjl.cn/questionBank/Upload/2019/02/09/10/12b67617/SYS201902091002258755809350_DA/SYS201902091002258755809350_DA.024.png" width="60" height="33" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> =，

所以与平面所成角的正弦值为．