Question

（2011•宁波模拟）如图，?ABCD中，AB=1，AD=2AB，∠ADC=60°，EC⊥面ABCD，EF∥AC，EF=

3

2

，CE=1
（1）求证：AF∥面BDE
（2）求CF与面DCE所成角的正切值．

Answer 1

分析：（1）要证AF∥面BDE，根据线面平行的判定定理，只需证明AF平行于面BDE中的一条直线，即证AF∥OE；
（2）先找出线面角，只需证明：EF⊥面DCE即可，再在△FCE中，利用正切函数可得结论．

解答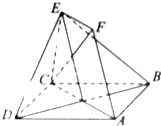：（1）证明：∵平行四边形ABCD中，AB=1，AD=2AB，∠ADC=60°
∴AC=

AD2+CD2-2AD•CDcos∠ADC

=

3

设O为AC与BD交点，
∵ABCD是平行四边形
∴O为AC与BD的中点
∴AO=

3

2

=EF，
∵EF∥AC
∴AO∥EF
∵AO=EF
∴EOAF为平行四边形，
∴OE∥AF
∵AF?面BDE，OE?面BDE
∴AF∥面BDE
（2）解：△ACD中，∵AD=2，AC=

3

，∠ADC=60°
∴

AC

sin∠ADC

=

AD

sin∠ACD

∴∠ACD=90°
∴AC⊥CD
∵AC∥EF
∴EF⊥CD
∵EC⊥面ABCD，AC?面ABCD，
∴EC⊥AC
∵AC∥EF
∴EF⊥EC
∵CD∩EC=C
∴EF⊥面DCE
∴∠FCE为CF与面DCE所成角
△FCE中，EF⊥CE，EF=

3

2

CE=1
∴tan∠FCE=

3

2

∴CF与面DCE所成角的正切值为

3

2

点评：本题以线面垂直为载体，考查线面平行，考查线面角，解题的根据是利用线面平行、线面垂直的判定定理，证明线面平行、线面垂直．