题目内容
若抛物线 的焦点与椭圆
的焦点与椭圆 的左焦点重合,则m的值为
的左焦点重合,则m的值为
- A.-

- B.

- C.-2
- D.2
A
分析:先确定抛物线与椭圆的焦点坐标,根据抛物线 的焦点与椭圆
的焦点与椭圆 的左焦点重合,可建立方程,从而可求m的值
的左焦点重合,可建立方程,从而可求m的值
解答:抛物线 的焦点坐标为
的焦点坐标为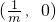
椭圆 ,∵a2=7,b2=3,
,∵a2=7,b2=3,
∴c2=a2-b2=4,
∴椭圆的左焦点坐标为(-2,0)
∵抛物线 的焦点与椭圆
的焦点与椭圆 的左焦点重合,
的左焦点重合,
∴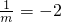
∴
故选A.
点评:本题重点考查圆锥曲线的几何性质,解题的关键是求出相应抛物线与椭圆的焦点坐标.
分析:先确定抛物线与椭圆的焦点坐标,根据抛物线
 的焦点与椭圆
的焦点与椭圆 的左焦点重合,可建立方程,从而可求m的值
的左焦点重合,可建立方程,从而可求m的值解答:抛物线
 的焦点坐标为
的焦点坐标为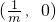
椭圆
 ,∵a2=7,b2=3,
,∵a2=7,b2=3,∴c2=a2-b2=4,
∴椭圆的左焦点坐标为(-2,0)
∵抛物线
 的焦点与椭圆
的焦点与椭圆 的左焦点重合,
的左焦点重合,∴
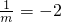
∴

故选A.
点评:本题重点考查圆锥曲线的几何性质,解题的关键是求出相应抛物线与椭圆的焦点坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的焦点与椭圆
的焦点与椭圆 的左焦点重合,则
的左焦点重合,则 的值为( )
的值为( ) B.
B. 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为
的值为
 的焦点与椭圆
的焦点与椭圆 的左焦点重合,则
的左焦点重合,则 的值为( )
的值为( ) D.
D.
 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为 .
的值为 . 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( ) B.2 C.
B.2 C. D.4
D.4