题目内容
设f(x)=1+x+(1+x)2+…+(1+x)n(x≠0,n∈N*)的展开式中x项的系数为Tn,则| lim |
| n→∞ |
| Tn |
| n2 |
分析:根据题意,分析可得,f(x)=(1+x)+(1+x)2+…+(1+x)n中x的系数分别为1、C21、C31、…Cn1,进而可求得则Tn,代入
,计算可得答案.
| lim |
| n→∞ |
| Tn |
| n2 |
解答:解:根据题意,f(x)=(1+x)+(1+x)2+…+(1+x)n中x的系数分别为1、C21、C31、…Cn1,
则Tn=1+C21+C31+…+Cn1=1+2+3+…+n=
;
则
=
,
故答案为
.
则Tn=1+C21+C31+…+Cn1=1+2+3+…+n=
| n(n+1) |
| 2 |
则
| lim |
| n→∞ |
| Tn |
| n2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查二项式的系数性质、数列求和与极限的计算,有一定难度,要灵活运用这几方面知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
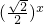 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1)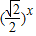 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)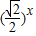 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)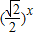 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)