题目内容
函数 的定义域为
的定义域为
- A.

- B.

- C.{x|2kπ≤x<2kπ+
 },k∈Z}∪{x|x=2kπ+π,k∈Z}
},k∈Z}∪{x|x=2kπ+π,k∈Z} - D.
 且x≠2kπ+π,k∈Z}
且x≠2kπ+π,k∈Z}
C
分析:要使函数有意义,则根据负数不能开偶次方根,即由 求解.
求解.
解答:由 即
即 (k∈Z)得,2kπ≤x<2kπ+
(k∈Z)得,2kπ≤x<2kπ+ (k∈Z)或x=2kπ+π,(k∈Z).
(k∈Z)或x=2kπ+π,(k∈Z).
所以函数y= 的定义域是
的定义域是
{x|2kπ≤x<2kπ+ ,k∈Z}∪{x|x=2kπ+π,k∈Z}.
,k∈Z}∪{x|x=2kπ+π,k∈Z}.
故选C.
点评:本题主要考查了定义域的常见类型一是负数不能开偶次根,涉及到三角不等式的解法,易错点在于忽视x=2kπ+π,k∈Z的情形,属于中档题.
分析:要使函数有意义,则根据负数不能开偶次方根,即由
 求解.
求解.解答:由
 即
即 (k∈Z)得,2kπ≤x<2kπ+
(k∈Z)得,2kπ≤x<2kπ+ (k∈Z)或x=2kπ+π,(k∈Z).
(k∈Z)或x=2kπ+π,(k∈Z).所以函数y=
 的定义域是
的定义域是{x|2kπ≤x<2kπ+
 ,k∈Z}∪{x|x=2kπ+π,k∈Z}.
,k∈Z}∪{x|x=2kπ+π,k∈Z}.故选C.
点评:本题主要考查了定义域的常见类型一是负数不能开偶次根,涉及到三角不等式的解法,易错点在于忽视x=2kπ+π,k∈Z的情形,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的定义域为[a,b],值域为[-2,1],则b-a的值不可能是 ( )
的定义域为[a,b],值域为[-2,1],则b-a的值不可能是 ( ) B.
B. C.
C. D.
D.
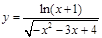 的定义域为
的定义域为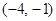 (B)
(B) 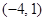 (C)
(C) 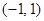 (D)
(D) 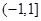
 的定义域为
的定义域为  B.
B.
 的定义域为( )
的定义域为( )
 B.
B. C.
C. D.
D.
