题目内容
直线y=kx+1与双曲线x2-y2=1的左支交于A、B两点，直线l经过点(-2,0)及AB中点，求直线l在y轴上截距b的取值范围.
解析：将y=kx+1代入双曲线方程x2-y2=1,
整理得(1-k2)x2-2kx-2=0. (*)
∵直线与双曲线左支交于两点，如图所示.
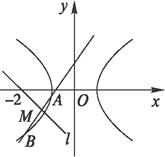
∴方程(*)有两相异负根.
∴
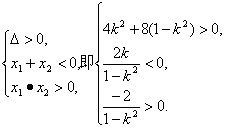
解得1＜k＜
,AB中点为(
).
∴直线l的斜率为
.∴l的方程为y=
.
令x=0，得b=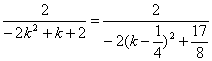
.
∵1＜k＜
,
∴
-2＜-2(k-
)2+
＜1.
∴b的范围是(-∞,-2-
)∪(2,+∞).
练习册系列答案
相关题目
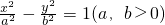的虚轴长为2
，渐近线方程是y=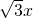
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且
．
的虚轴长为2
，渐近线方程是y=
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且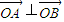
．