题目内容
在正三棱锥S-ABC中,SA=1,∠ASB=40°,过A作三棱锥的截面AMN,则截面三角形AMN的 周长的最小值为
.
| 3 |
| 3 |
分析:因为截面周长为三条线段之和,而当线段共线时,和最小,所以可考虑把三棱锥展开,则AA1的长度,即为截面三角形的最小周长.再放入三角形中,解三角形即可得到截面周长的最小值.
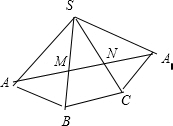
解答:解:沿侧棱S把正三棱锥的侧面展开如右图,
可观察出,当截与三棱锥各面交线恰好共线时,周长最小,
且最小值为AA1的长,
在△AA1S中,SA=SA1=1,∠ASA1=120°
∴AA12=SA2+SA12-2SA•SA1cos120°
=1+1+1=3
∴AA1=
故答案为
可观察出,当截与三棱锥各面交线恰好共线时,周长最小,
且最小值为AA1的长,
在△AA1S中,SA=SA1=1,∠ASA1=120°
∴AA12=SA2+SA12-2SA•SA1cos120°
=1+1+1=3
∴AA1=
| 3 |

故答案为
| 3 |
点评:本题主要考查了正三棱锥的侧面展开图的性质,充分考查了学生的空间想象力,逻辑推理能力,以及计算能力

练习册系列答案
相关题目
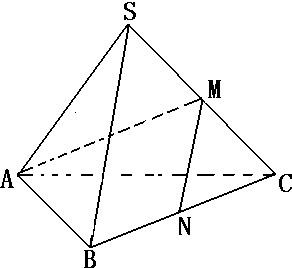 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|