题目内容
已知f(x+1)=xα(α为常数),且函数y=f(x)的图象经过点(5,2).
(1)求f(x)的解析式;(2)用单调性定义证明y=f(x)在定义域内为增函数.
解:(1)∵f(x+1)=xα∴f(x)=(x-1)α,
又y=f(x)的图象过点(5,2)∴f(5)=(5-1)α=2,α=log42=
∴ (x≥1)
(x≥1)
(2)设1≤x1<x2,
则f(x1)-f(x2)= =
=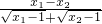 <0
<0
∴f(x1)<f(x2)∴y=f(x)在定义域内为增函数.
分析:(1)先根据f(x+1)=xα表示出f(x),然后将点(5,2)代入,求出α,从而求出函数f(x)的解析式;
(2)设1≤x1<x2,然后通过化简变形判定f(x1)-f(x2)的符号,根据增函数的定义进行判定即可.
点评:本题主要考查了幂函数,以及函数单调性的判断与证明,解题的关键就是对f(x1)-f(x2)进行化简变形定号,属于基础题.
又y=f(x)的图象过点(5,2)∴f(5)=(5-1)α=2,α=log42=

∴
 (x≥1)
(x≥1)(2)设1≤x1<x2,
则f(x1)-f(x2)=
 =
=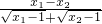 <0
<0∴f(x1)<f(x2)∴y=f(x)在定义域内为增函数.
分析:(1)先根据f(x+1)=xα表示出f(x),然后将点(5,2)代入,求出α,从而求出函数f(x)的解析式;
(2)设1≤x1<x2,然后通过化简变形判定f(x1)-f(x2)的符号,根据增函数的定义进行判定即可.
点评:本题主要考查了幂函数,以及函数单调性的判断与证明,解题的关键就是对f(x1)-f(x2)进行化简变形定号,属于基础题.

练习册系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.