题目内容
 如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为
如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 4 |
| 5 |
(Ⅰ)求元件A不正常工作的概率;
(Ⅱ)求元件A、B、C都正常工作的概率;
(Ⅲ)求系统N正常工作的概率.
分析:(Ⅰ)元件A不正常工作是元件A正常工作的对立事件,所以元件A不正常工作的概率为1减去正常工作的概率;
(Ⅱ)元件A、B、C都正常工作是三个相互独立事件同时发生;
(Ⅲ)系统N正常工作可分为A、B、C都正常工作和A、D正常但B、C不都正常工作两种情况,概率是两种情况的概率和.
(Ⅱ)元件A、B、C都正常工作是三个相互独立事件同时发生;
(Ⅲ)系统N正常工作可分为A、B、C都正常工作和A、D正常但B、C不都正常工作两种情况,概率是两种情况的概率和.
解答:解:设元件A正常工作为事件A,元件B正常工作为事件B,元件C正常工作为事件C,元件D正常工作为事件D.
(Ⅰ)由元件A正常工作的概率P(A)=
,所以它不正常工作的概率P(
)=1-P(A)=
;
(Ⅱ)元件A、B、C都正常工作的概率P(A•B•C)=P(A)P(B)P(C)=
•
•
=
;
(Ⅲ)系统N正常工作可分为A、B、C都正常工作和A、D正常但B、C不都正常工作两种情况,
A、B、C都正常工作的概率为
,
A、D正常但B、C不都正常工作的概率为P(A•
•C•
)+P(A•B•
•D)+P(A•
•
•D)=
•
•
•
+
•
•
•
+
•
•
•
=
,
所以系统N正常工作的概率是
+
=
.
(Ⅰ)由元件A正常工作的概率P(A)=
| 2 |
| 3 |
. |
| A |
| 1 |
| 3 |
(Ⅱ)元件A、B、C都正常工作的概率P(A•B•C)=P(A)P(B)P(C)=
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
(Ⅲ)系统N正常工作可分为A、B、C都正常工作和A、D正常但B、C不都正常工作两种情况,
A、B、C都正常工作的概率为
| 3 |
| 8 |
A、D正常但B、C不都正常工作的概率为P(A•
. |
| B |
. |
| D |
. |
| C |
. |
| B |
. |
| C |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4 |
| 5 |
| 7 |
| 30 |
所以系统N正常工作的概率是
| 3 |
| 8 |
| 7 |
| 30 |
| 73 |
| 120 |
点评:本题考查了相互独立事件的概率乘法公式,解答此题的关键是熟记公式,并且能够正确分类,特别是(Ⅲ)中的两种情况,要做到不重不漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

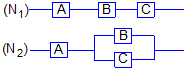 如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80、0.90、0.90.分别求系统N1、N2正常工作的概率P1、P2.
如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80、0.90、0.90.分别求系统N1、N2正常工作的概率P1、P2.
