题目内容
已知定义域为(-1,1)的函数f(x)=
.
(Ⅰ)判断函数f(x)奇偶性并加以证明;
(Ⅱ)判断函数f(x)的单调性并用定义加以证明;
(Ⅲ)解关于x的不等式f(x-1)+f(x)<0.
| x |
| x2+1 |
(Ⅰ)判断函数f(x)奇偶性并加以证明;
(Ⅱ)判断函数f(x)的单调性并用定义加以证明;
(Ⅲ)解关于x的不等式f(x-1)+f(x)<0.
(I)f(x)为定义域上的奇函数,证明如下:
定义域为(-1,1),关于原点对称,
又f(-x)=
=
=-f(x),
∴f(x)为奇函数;
(II)f(x)在(-1,1)上单调递增,证明如下:
任取x1,x2∈(-1,1),且x1<x2,
则f(x1)-f(x2)=
-
=
=
,
∵x1,x2∈(-1,1),且x1<x2,
∴x2-x1>0,x1x2-1<0,x12+1>0,x22+1>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-1,1)上单调递增;
(III)由(Ⅰ)知,f(x)为奇函数,
∴f(x-1)+f(x)<0等价于f(x-1)<-f(x)=f(-x),
由(Ⅱ)知f(x)单调递增,
∴
,解得0<x<
,
∴不等式的解集为:(0,
);
定义域为(-1,1),关于原点对称,
又f(-x)=
| -x |
| (-x)2+1 |
| -x |
| x2+1 |
∴f(x)为奇函数;
(II)f(x)在(-1,1)上单调递增,证明如下:
任取x1,x2∈(-1,1),且x1<x2,
则f(x1)-f(x2)=
| x1 |
| x12+1 |
| x2 |
| x22+1 |
=
| x1(x22+1)-x2(x12+1) |
| (x12+1)(x22+1) |
=
| (x2-x1)(x1x2-1) |
| (x12+1)(x22+1) |
∵x1,x2∈(-1,1),且x1<x2,
∴x2-x1>0,x1x2-1<0,x12+1>0,x22+1>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-1,1)上单调递增;
(III)由(Ⅰ)知,f(x)为奇函数,
∴f(x-1)+f(x)<0等价于f(x-1)<-f(x)=f(-x),
由(Ⅱ)知f(x)单调递增,
∴
|
| 1 |
| 2 |
∴不等式的解集为:(0,
| 1 |
| 2 |

练习册系列答案
相关题目
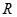 上函数
上函数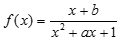 为奇函数.
为奇函数.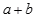 的值;
的值;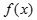 的值域.
的值域.