题目内容
各项均为正数的等比数列{an}满足a1a7=4,a6=8,函数f(x)=a1x+a2x2+a3x3+…+a10x10,则f( )= .
)= .
【答案】分析:正数的等比数列{an}满足a1a7=4,a6=8,可以求出等比数列的通项公式,根据函数f(x)=a1x+a2x2+a3x3+…+a10x10,求出通项bn=anxn,从而进行求解;
解答:解:∵正数的等比数列{an}满足a1a7=4,∴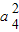 =4,可得a4=2,
=4,可得a4=2,
∵a6=8,
∴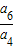 =q2,可得q2=4,可得q=2,∴a1×q3=2,得a1=
=q2,可得q2=4,可得q=2,∴a1×q3=2,得a1= ,
,
∴an=a1×qn= ×2n-1=2n-3,
×2n-1=2n-3,
∴f(x)=a1x+a2x2+a3x3+…+a10x10,
∴f( )=a1
)=a1 +a2
+a2 2+a3(
2+a3( )3+…+a10(
)3+…+a10( )10=
)10=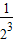 +
+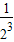 +…+
+…+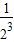 =10×
=10×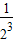 =
=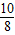 =
= ,
,
故答案为 ;
;
点评:此题主要考查等比数列的性质及其应用,综合性比较强,计算量也比较大,解题的关键是求出等比数列的通项公式;
解答:解:∵正数的等比数列{an}满足a1a7=4,∴
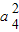 =4,可得a4=2,
=4,可得a4=2,∵a6=8,
∴
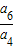 =q2,可得q2=4,可得q=2,∴a1×q3=2,得a1=
=q2,可得q2=4,可得q=2,∴a1×q3=2,得a1= ,
,∴an=a1×qn=
 ×2n-1=2n-3,
×2n-1=2n-3,∴f(x)=a1x+a2x2+a3x3+…+a10x10,
∴f(
 )=a1
)=a1 +a2
+a2 2+a3(
2+a3( )3+…+a10(
)3+…+a10( )10=
)10=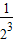 +
+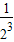 +…+
+…+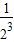 =10×
=10×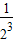 =
=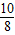 =
= ,
,故答案为
 ;
;点评:此题主要考查等比数列的性质及其应用,综合性比较强,计算量也比较大,解题的关键是求出等比数列的通项公式;

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目