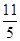题目内容
设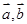 为非零向量,
为非零向量,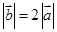 ,两组向量
,两组向量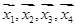 和
和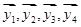 均由2个
均由2个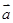 和2个
和2个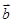 排列而成,若
排列而成,若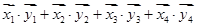 所有可能取值中的最小值为
所有可能取值中的最小值为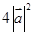 ,则
,则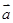 与
与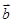 的夹角为( )
的夹角为( )
A.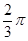 | B.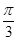 | C.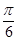 | D.0 |
B
解析试题分析:由题意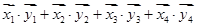 有以下三种可能:①
有以下三种可能:①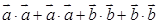
 ;②
;②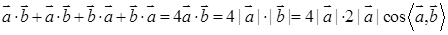
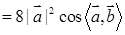 ;③
;③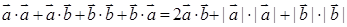
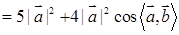 ,已知第②种情况原式的值最小,即
,已知第②种情况原式的值最小,即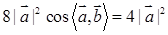 ,解得
,解得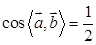 ,即
,即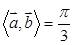 ,故选B.
,故选B.
考点:1.向量的数量积运算;2.分类讨论思想的应用.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
设向量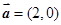 ,
,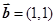 ,则下列结论中正确的是
,则下列结论中正确的是
A.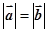 | B.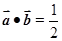 | C.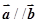 | D.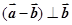 |
平面向量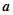 与
与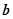 的夹角为60°,
的夹角为60°,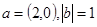 ,则
,则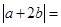 ( )
( )
A.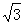 | B. | C.4 | D.12 |
 中,
中,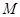 是线段
是线段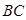 的中点且
的中点且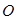 是线段
是线段 上一个动点,若
上一个动点,若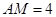 ,则
,则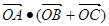 的最小值为( )
的最小值为( )
A.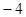 | B.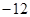 | C.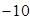 | D.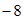 |
平面上有四个互异的点A,B,C,D,满足( -
- )·(
)·(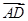 -
-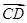 )=0,则△ABC是( )
)=0,则△ABC是( )
| A.直角三角形 | B.等腰三角形 |
| C.等腰直角三角形 | D.等边三角形 |
[2013·重庆诊测]若向量a=(1,λ,2),b=(2,-1,2),且a与b的夹角余弦值为 ,则λ等于( )
,则λ等于( )
| A.2 | B.-2 | C.-2或 | D.2或- |
对任意两个非零的平面向量α和β,定义 .若两个非零的平面向量
.若两个非零的平面向量 和
和 ,满足
,满足 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,则
中,则 =
=
A. | B. | C.1 | D. |
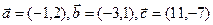 ,且
,且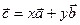 ,求
,求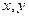 的值.
的值. -t
-t )·
)·