题目内容
 三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,PA=AC,则直线PC与平面PAB所成的角是( )
三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,PA=AC,则直线PC与平面PAB所成的角是( )分析:由PA⊥平面ABC证出PA⊥AC,结合AB⊥AC可得AC⊥平面PAB,所以∠APC是直线PC与平面PAB所成的角.然后根据Rt△PAC是等腰直角三角形,可得∠APC=45°,即得直线PC与平面PAB所成角的大小.
解答:解:∵PA⊥平面ABC,AC?平面ABC,
∴PA⊥AC
又∵AB⊥AC,PA、AB是平面PAB内的相交直线
∴AC⊥平面PAB,
由此可得∠APC就是直线PC与平面PAB所成的角
∵Rt△PAC中,∠PAC=90°,PA=AC,
∴∠APC=45°,即得直线PC与平面PAB所成的角等于45°
故选:C
∴PA⊥AC
又∵AB⊥AC,PA、AB是平面PAB内的相交直线
∴AC⊥平面PAB,
由此可得∠APC就是直线PC与平面PAB所成的角
∵Rt△PAC中,∠PAC=90°,PA=AC,
∴∠APC=45°,即得直线PC与平面PAB所成的角等于45°
故选:C
点评:本题在特殊三棱锥中,求直线与平面所成角的大小.着重考查了直线与平面垂直的判定与性质、直线与平面所成角的定义及求法等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.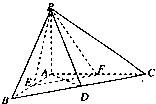 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,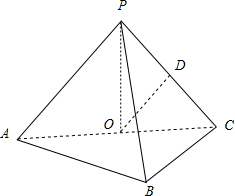 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.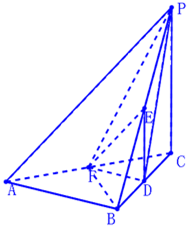 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.