Question

某营养师要为某个儿童预订午餐和晚餐，已知一个单位的午餐含个单位的碳水化合物，个单位的蛋白质和个单位的维生素；一个单位的晚餐含个单位的碳水化合物，个单位的蛋白质和个单位的维生素.另外，该儿童这两餐需要的营养中至少含个单位的碳水化合物，个单位的蛋白质和个单位的维生素.如果一个单位的午餐、晚餐的费用分别是元和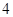元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？

Answer 1

应当为该儿童预订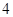个单位的午餐和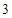个单位的晚餐，就可满足要求．

解析试题分析：先根据条件列举出、所满足的约束条件，并确定目标函数，然后作出可行域，利用目标函数所代表的直线进行平移，根据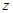的几何意义确定最优解，从而解决实际问题.
试题解析：设需要预订满足要求的午餐和晚餐分别为个单位和个单位，所花的费用为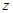元，
则依题意得：，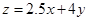
且、满足：
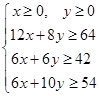，即，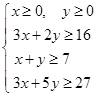
画出可行域如图所示：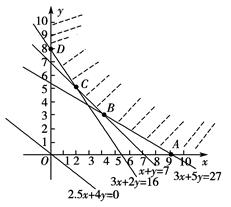

让目标函数表示的直线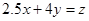在可行域上平移，
由此可知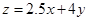在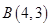处取得最小值．
因此，应当为该儿童预订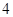个单位的午餐和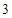个单位的晚餐，就可满足要求．
考点：线性规划