题目内容
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的动圆恒与
的动圆恒与![]() 轴相切,
轴相切,![]() 为该圆的直径,设点
为该圆的直径,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的任意直线
的任意直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,除
,除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?说明理由.
是否有其它公共点?说明理由.
【答案】(1)![]() ;(2)没有其他公共点,证明见解析
;(2)没有其他公共点,证明见解析
【解析】
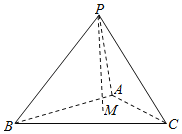
(1)如图所示:作![]() 轴于
轴于![]() ,
,![]() 直线
直线![]() 于
于![]() ,
,![]() 轴于
轴于![]() ,计算得到
,计算得到![]() ,根据抛物线定义得到答案.
,根据抛物线定义得到答案.
(2)![]() 在抛物线上,设
在抛物线上,设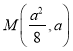 ,得到直线
,得到直线![]() :
:![]() ,联立方程得到答案.
,联立方程得到答案.
(1)如图所示:作![]() 轴于
轴于![]() ,
,![]() 直线
直线![]() 于
于![]() ,
,![]() 轴于
轴于![]() ,
,
设圆半径为![]() ,在梯形
,在梯形![]() 中,
中,![]() 为中位线,故
为中位线,故![]() ,故
,故![]() .
.
故![]() ,
,![]() ,即
,即![]() ,根据抛物线定义知:
,根据抛物线定义知:![]() .
.
(2)没有其他公共点.![]() 在抛物线上,设
在抛物线上,设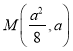 ,故
,故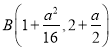 .
.
故当![]() 时,
时,![]() ,故
,故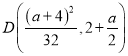 ,
,
故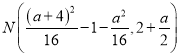 ,即
,即![]() .
.
 ,(
,(![]() ),直线
),直线![]() :
:![]() .
.
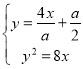 ,故
,故![]() ,故方程有唯一解,故没有其他公共点.
,故方程有唯一解,故没有其他公共点.
当![]() 时验证知,
时验证知,![]() 为
为![]() 轴,也没有其他公共点.
轴,也没有其他公共点.
综上所述:没有其他公共点.
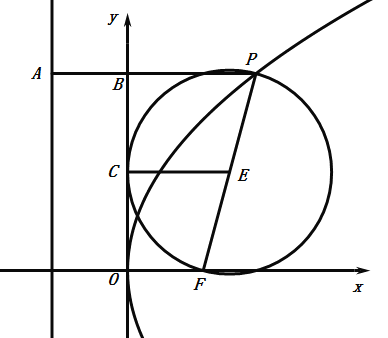

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目