Question

（2013•石景山区二模）如图，椭圆C：x2+

y2

m

=1  (0＜m＜1)的左顶点为A，M是椭圆C上异于点A的任意一点，点P与点A关于点M对称．
（Ⅰ）若点P的坐标为(

9

5

，

4 3

5

)，求m的值；
（Ⅱ）若椭圆C上存在点M，使得OP⊥OM，求m的取值范围．

Answer 1

分析：（Ⅰ）由题意知M是线段AP的中点，由中点坐标公式可得M坐标，代入椭圆方程即可得到m值；
（Ⅱ）设M（x₀，y₀）（-1＜x₀＜1），则 

x

2 0

+

y 2 0

m

=1，①由中点坐标公式可用M坐标表示P点坐标，由OP⊥OM得

OP

•

OM

=0②，联立 ①②消去y₀，分离出m用基本不等式即可求得m的范围；

解答：解：（Ⅰ）依题意，M是线段AP的中点，

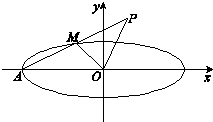
因为A（-1，0），P(

9

5

，

4 3

5

)，
所以 点M的坐标为(

2

5

，

2 3

5

)．
由于点M在椭圆C上，
所以 

4

25

+

12

25m

=1，解得 m=

4

7

．
（Ⅱ）设M（x₀，y₀）（-1＜x₀＜1），则 

x

2 0

+

y 2 0

m

=1，①
因为 M是线段AP的中点，所以 P（2x₀+1，2y₀）．
因为 OP⊥OM，所以

OP

⊥

OM

，
所以

OP

•

OM

=0，即 x0(2x0+1)+2y02=0．②
由 ①，②消去y₀，整理得 m=

2 x 2 0 +x0

2 x 2 0 -2

．
所以 m=1+

1

2(x0+2)+ 6 x0+2 -8

≤

1

2

-

3

4

，
当且仅当 x0=-2+

3

时，上式等号成立．
所以m的取值范围是(0，

1

2

-

3

4

]．

点评：本题考查直线与圆锥曲线位置关系、椭圆的简单性质，属中档题，垂直问题转化为向量的数量积为0是常用手段，要灵活运用．