题目内容
已知P是正六边形ABCDEF外一点，O为ABCDEF的中心，则
+
+
+
+
+
等于（ ）
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
A、
| ||
B、3
| ||
C、6
| ||
| D、0 |
分析：根据正六边形的性质，可得PO是△PAD、△PBE、△PCF公共的中线，由此可得
=
（
+
）=
（
+
）=
（
+
），化简整理即可得到
+
+
+
+
+
=6
，得到本题答案．
| PO |
| 1 |
| 2 |
| PA |
| PD |
| 1 |
| 2 |
| PB |
| PE |
| 1 |
| 2 |
| PC |
| PF |
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
| PO |
解答：解：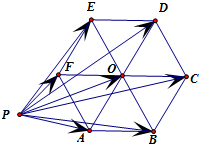
∵六边形ABCDEF是正六边形
∴对角线AD、BE、CF交于同一点O，且0是ABCDEF的中心
∵△PAD中，PO是AD边的中线，
∴
=
（
+
）
同理可得
=
（
+
），
=
（
+
）
3个式子相加可得：3
=
（
+
+
+
+
+
）
化简得
+
+
+
+
+
=6
故选：C
∵六边形ABCDEF是正六边形∴对角线AD、BE、CF交于同一点O，且0是ABCDEF的中心
∵△PAD中，PO是AD边的中线，
∴
| PO |
| 1 |
| 2 |
| PA |
| PD |
同理可得
| PO |
| 1 |
| 2 |
| PB |
| PE |
| PO |
| 1 |
| 2 |
| PC |
| PF |
3个式子相加可得：3
| PO |
| 1 |
| 2 |
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
化简得
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
| PO |
故选：C
点评：本题给出正六边形ABCDEF，要我们化简向量
+
+
+
+
+
，着重考查了平面向量的线性运算法则和正六边形的性质等知识，属于基础题．
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
练习册系列答案
阅读快车系列答案
相关题目
