题目内容
在△ABC中,若 ,则△ABC的形状为
,则△ABC的形状为
- A.直角三角形
- B.等腰三角形
- C.等边三角形
- D.等腰直角三角形
C
分析:先由向量垂直的条件得 ,即
,即 ,同理得:
,同理得: ,得到:AB=AC,再由余弦定理得:cosA=
,得到:AB=AC,再由余弦定理得:cosA= ,从而有
,从而有 =
= ,?a=b.最后综上所述,△ABC的形状为等边三角形.
,?a=b.最后综上所述,△ABC的形状为等边三角形.
解答:∵ ,
,
∴ ,
,
即 ,
,
又∵ 同理得:
同理得:
 ,
,
∴ =
= ,∴AB=AC,
,∴AB=AC,
代入 得:
得: ,
,
设AB=c,AC=b,BC=a,
∴cosA= 且c=b
且c=b
由余弦定理得:
cosA= ,
,
∴ =
= ,?a=b.
,?a=b.
综上所述,△ABC的形状为等边三角形
故选C.
点评:本题主要考查了向量在几何中的实际应用,考查了学生的计算能力和对向量的综合掌握,属于基础题.
分析:先由向量垂直的条件得
 ,即
,即 ,同理得:
,同理得: ,得到:AB=AC,再由余弦定理得:cosA=
,得到:AB=AC,再由余弦定理得:cosA= ,从而有
,从而有 =
= ,?a=b.最后综上所述,△ABC的形状为等边三角形.
,?a=b.最后综上所述,△ABC的形状为等边三角形.解答:∵
 ,
,∴
 ,
,即
 ,
,又∵
 同理得:
同理得: ,
,∴
 =
= ,∴AB=AC,
,∴AB=AC,代入
 得:
得: ,
,设AB=c,AC=b,BC=a,
∴cosA=
 且c=b
且c=b由余弦定理得:
cosA=
 ,
,∴
 =
= ,?a=b.
,?a=b.综上所述,△ABC的形状为等边三角形
故选C.
点评:本题主要考查了向量在几何中的实际应用,考查了学生的计算能力和对向量的综合掌握,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,则B的值为( )
,则B的值为( )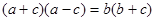 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.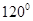 D.
D.
 ,则∠A=
,则∠A= 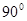 B.
B.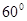 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2