题目内容
如图，四棱锥P—ABCD中，AB⊥AD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M为PC的中点.(1)求证：BM∥平面PAD；
(2)在△PAD内找一点N，使MN⊥平面PBD，并说明理由；?
(3)求二面角M-PB-D的大小.
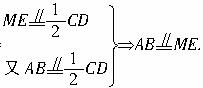
(1)证明：取PD的中点为E，连结AE、ME，由M是PC的中点得
?
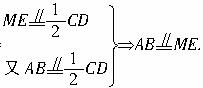所以四边形MBAE是平行四边形
BM∥AE，而AE
平面PAD,故BM∥平面PAD.
(2)解：取AE的中点为N，易知AE⊥平面PCD，即N在平面PCD上的射影为E.?
∴由三垂线定理得MN⊥PD.?
又M在底面ABCD上的射影为F，则F为AC的中点，N在底面ABCD上的射影为G，则AG=
AD=
.
易知FG⊥BD
MN⊥BD.?
故MN⊥平面PBD. ?
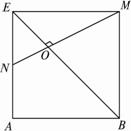
(3)解：如图，矩形BMEA中，EM=1，AE=
，MN与BE的交点为O，?
则O为M在平面PBD上的射影，tan∠NME=
=
cos∠NME=
，?
∴MO=MEcOs∠NME=
.?
过O作OQ⊥PB，由三垂线定理知MQ⊥PB，则∠MQO是二面角M-PB-D的平面角，易求MQ=
,即sin∠MQO=
=
.故二面角M-PB-D的大小为arcsin
.
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=