题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,且m=(a、b),n=(cosA、cosB),P=(2 sin
sin ,2sinA),若m∥n,p2=9,试判断三角形的形状.
,2sinA),若m∥n,p2=9,试判断三角形的形状.
解:∵ ∥
∥ ,
,
∴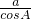 =
= 即acosB-bcosA=0,由正弦定理得:sinAcosB-cosAsinB=0,
即acosB-bcosA=0,由正弦定理得:sinAcosB-cosAsinB=0,
∴sin(A-B)=0,∴A=B,
∵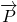 =(2
=(2 sin
sin ,2sinA)且
,2sinA)且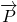 2=
2= =9,又
=9,又 =
= -
- ,
,
∴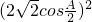 +(2sinA)2=9,即8
+(2sinA)2=9,即8 +4sin2A=9,
+4sin2A=9,
化简得:cosA= ,由A∈(0,π),得到A=
,由A∈(0,π),得到A= ,
,
∴A=B=C= ,
,
∴△ABC为等边三角形.
分析:根据向量平行时,向量的坐标满足的条件得到一个关系式,利用正弦定理化简此关系式得到sin(A-B)的值等于0,根据A与B为三角形的内角,得到A等于B,又利用模的计算法则表示出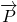 的平方,让其等于9,利用诱导公式及同角三角函数间的基本关系化简后,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,即可得到B的度数,进而得到C的度数,即可判断三角形ABC的形状.
的平方,让其等于9,利用诱导公式及同角三角函数间的基本关系化简后,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,即可得到B的度数,进而得到C的度数,即可判断三角形ABC的形状.
点评:本题是向量和三角函数相结合的题目,既考查了向量的基本知识,又考查了三角函数的有关知识,三角形的形状既可由角确定,又可由边确定,因此既可从角入手,把边化为角;也可从边入手,把角化为边来判断三角形的形状.
 ∥
∥ ,
,∴
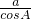 =
= 即acosB-bcosA=0,由正弦定理得:sinAcosB-cosAsinB=0,
即acosB-bcosA=0,由正弦定理得:sinAcosB-cosAsinB=0,∴sin(A-B)=0,∴A=B,
∵
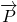 =(2
=(2 sin
sin ,2sinA)且
,2sinA)且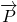 2=
2= =9,又
=9,又 =
= -
- ,
,∴
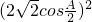 +(2sinA)2=9,即8
+(2sinA)2=9,即8 +4sin2A=9,
+4sin2A=9,化简得:cosA=
 ,由A∈(0,π),得到A=
,由A∈(0,π),得到A= ,
,∴A=B=C=
 ,
,∴△ABC为等边三角形.
分析:根据向量平行时,向量的坐标满足的条件得到一个关系式,利用正弦定理化简此关系式得到sin(A-B)的值等于0,根据A与B为三角形的内角,得到A等于B,又利用模的计算法则表示出
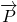 的平方,让其等于9,利用诱导公式及同角三角函数间的基本关系化简后,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,即可得到B的度数,进而得到C的度数,即可判断三角形ABC的形状.
的平方,让其等于9,利用诱导公式及同角三角函数间的基本关系化简后,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,即可得到B的度数,进而得到C的度数,即可判断三角形ABC的形状.点评:本题是向量和三角函数相结合的题目,既考查了向量的基本知识,又考查了三角函数的有关知识,三角形的形状既可由角确定,又可由边确定,因此既可从角入手,把边化为角;也可从边入手,把角化为边来判断三角形的形状.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|