题目内容
(1)已知 ,
,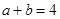 ,求证:
,求证: ;
;
(2)已知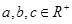 ,
,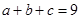 ,求证:
,求证: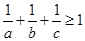 ;
;
并类比上面的结论写出推广后的一般性结论(不需证明).
(1)证明书详见解析;(2)证明详见解析;(3)结论推广为: ,则
,则 .
.
解析试题分析:(1)由均值不等式 即可证明
即可证明 ;(2)注意到:
;(2)注意到: ,故可考虑用柯西不等式得到
,故可考虑用柯西不等式得到 ,进而得出所要证明的不等式;(3)观察(1)(2)所给条件
,进而得出所要证明的不等式;(3)观察(1)(2)所给条件 ,
, ,可想到任意
,可想到任意 个正数的条件为
个正数的条件为 ,而(1)(2)的结论都是对应数的倒数之和大于等于1,所以结论为:
,而(1)(2)的结论都是对应数的倒数之和大于等于1,所以结论为: .
.
(1)因为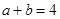 且
且
所以由基本不等式 可得
可得 ,再根据倒数法则可得
,再根据倒数法则可得 ;
;
(2)因为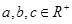 ,
,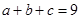
所以由柯西不等式可得 即
即 ,所以
,所以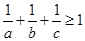
(3)一般性结论为: ,则
,则 .
.
考点:1.基本不等式;2.柯西不等式;3.归纳推理.

练习册系列答案
相关题目
已知区域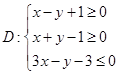 的面积为
的面积为 ,点集
,点集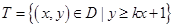 在坐标系中对应区域的面积为
在坐标系中对应区域的面积为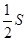 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
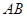 、
、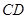 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知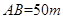 ,
,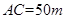 ,当
,当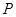 为
为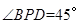 .
.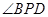 达到最大.
达到最大.
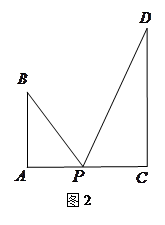
 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆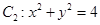 的直径,
的直径,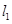 、
、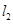 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中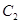 于
于 、
、 两点,
两点, .
.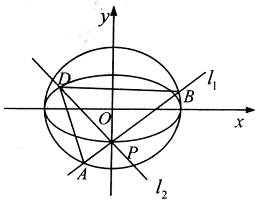
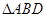 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线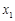 ,
, ,
,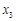 为正实数,若
为正实数,若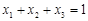 ,求证:
,求证: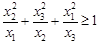 .
.
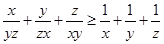 .
. 对于一切正数
对于一切正数 、
、 恒成立,则实数
恒成立,则实数 的最小值为
的最小值为