Question

如图，三棱锥P―ABC中，PA⊥AB，PA⊥AC，AB⊥AC，PA=AC=2，AB=1，M为PC的中点。

   （1）求证：平面PCB⊥平面MAB；

   （2）求点A到平面PBC的距离；

   （3）求二面角C―PB―A的正切值.

Answer 1

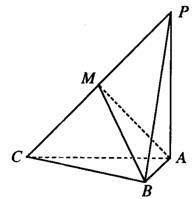
方法一：（1）∵PA⊥AB，AB⊥AC

∴AB⊥平面PAC，故AB⊥PC

∵PA=AC=2，M为PC的中点

∴MA⊥PC

∴PC⊥平面MAB

又PC平面PCB，

所以平面PCB⊥平面MAB

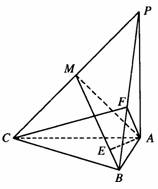
（2）如图，在平面MAB中作AE⊥MB，垂足是E

∵平面PCB⊥平面MAB

平面PCB∩平面MAB=MB

∴AE⊥平面PBC

∴AE的长为点A到平面PBC的距离

又∵AB⊥平面PAC，∴AB⊥AM

∴在直角三角形ABM中，

∴AE?MB=AB?AM，

∴AE=即为所求

（3）在平面PAB中作AF⊥PB，垂足是F，连接CF

∵PA⊥AC，AB⊥AC

∴AC⊥平面PAB

则AC⊥AF，且AF是CF在平面PAB内的射影，

∴CF⊥PB（三垂线定理）

∴∠AFC是二面角C―PB―A的平面角，

在直角三角形PAB中，PA=2，AB=1

∴在直角三角形AFC中，

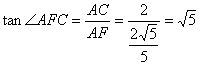即为所求

方法二：（1）同方法一

（2）以A为原点，建立如图的空间直角坐标系，由已知可得各点坐标为

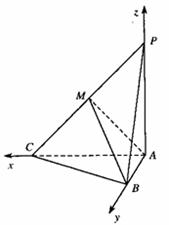A（0，0，0），B（0，1，0）C（2，0，0），P（0，0，2），M（1，0，1）

设平面PBC的法向量为n=（x，y，z），且

（3）∵PA⊥AC，AB⊥AC

∴AC⊥平面PAB

∴平面PAB的法向量为

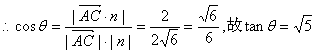即为所求