题目内容
已知关于x的实系数一元二次不等式ax2+bx+c≥0(a<b)的解集为R,则M=
的最小值是
| a+3b+4c |
| b-a |
2
+5
| 5 |
2
+5
.| 5 |
分析:由题意可得4ac≥b2,而M=
≥
=
,令
=t,M可化为M=(t-1)+
+5,下由基本不等式可得.
| a2+3ab+4ac |
| a(b-a) |
| a2+3ab+b2 |
| ab-a2 |
1+3•
| ||||
|
| b |
| a |
| 5 |
| t-1 |
解答:解:由题意,ax2+bx+c≥0(a<b)的解集为R,
则必有△=b2-4ac≤0,a>0,即4ac≥b2
对于M=
,分子、分母同乘a可得,
M=
≥
=
令
=t,∵a<b,a>0,∴t>1,
故M=
=
=(t-1)+
+5
≥2
+5=2
+5,当且仅当t=
+1,即b=(
+1)a时等号成立,
故答案为:2
+5
则必有△=b2-4ac≤0,a>0,即4ac≥b2
对于M=
| a+3b+4c |
| b-a |
M=
| a2+3ab+4ac |
| a(b-a) |
| a2+3ab+b2 |
| ab-a2 |
1+3•
| ||||
|
令
| b |
| a |
故M=
| t2+3t+1 |
| t-1 |
| (t-1)2+5(t-1)+5 |
| t-1 |
| 5 |
| t-1 |
≥2
(t-1)
|
| 5 |
| 5 |
| 5 |
故答案为:2
| 5 |
点评:本题为基本不等式求最值,涉及二次不等式恒成立以及代数式的变形,属基础题.

练习册系列答案
相关题目
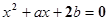 的一根在
的一根在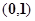 内,另一根在
内,另一根在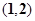 内,则点
内,则点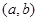 所在区域的面积为
所在区域的面积为 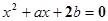 的一根在
的一根在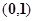 内,另一根在
内,另一根在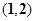 内,则点
内,则点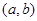 所在区域的面积为
所在区域的面积为