题目内容
已知a、b、c为三角形ABC中角A、B、C的对边,且a2-a-2b-2c=0,a+2b-2c+3=0,求这个三角形的最大内角.
【答案】分析:先将b、c用a表示,然后判定a、b、c的大小,根据大边对大角,最后根据余弦定理求出最大内角即可.
解答:解:因为a2-a-2b-2c=0,a+2b-2c+3=0,所以a2-a-2b-(a+2b+3)=0
所以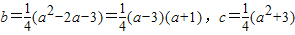 ------------(3分)
------------(3分)
因为b>0,所以a2-2a-3>0,所以a>3,------------(5分)
所以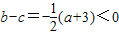 ,
,
即b<c ①--------(7分)
又c-a=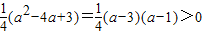 ,
,
所以c>a ②.由①②可得c边最大.---------(8分)
在三角形ABC中,有余弦定理得: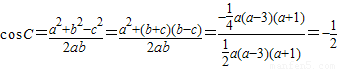
所以C=120°,即三角形的最大内角为120---------(11分)
点评:本题主要考查了三角形的边角关系,余弦定理以及特殊角的三角函数值,利用作差的方法得到c为最大边是解题的关键,同时考查了利用了消元的思想,属于中档题.
解答:解:因为a2-a-2b-2c=0,a+2b-2c+3=0,所以a2-a-2b-(a+2b+3)=0
所以
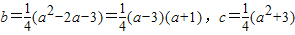 ------------(3分)
------------(3分)因为b>0,所以a2-2a-3>0,所以a>3,------------(5分)
所以
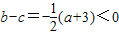 ,
,即b<c ①--------(7分)
又c-a=
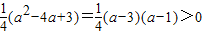 ,
,所以c>a ②.由①②可得c边最大.---------(8分)
在三角形ABC中,有余弦定理得:
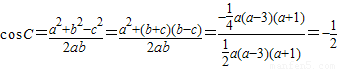
所以C=120°,即三角形的最大内角为120---------(11分)
点评:本题主要考查了三角形的边角关系,余弦定理以及特殊角的三角函数值,利用作差的方法得到c为最大边是解题的关键,同时考查了利用了消元的思想,属于中档题.

练习册系列答案
相关题目
 ,则△ABC为( )
,则△ABC为( ) ,则△ABC为( )
,则△ABC为( )