题目内容
矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1,BC边上存在点Q,使得PQ⊥QD,求a的取值范围.分析:由三垂线的性质知,AQ⊥QD,所以,点Q在以线段AD为直径的圆上,又点Q在BC边上,所以,
≥1;计算可得答案.
| a |
| 2 |
解答:解:∵PA⊥平面AC,∴AQ是 PQ在面ABCD的射影,
∵PQ⊥QD,∴AQ⊥QD,
∴点Q在以线段AD为直径的圆上,圆的半径为
,
又点Q在BC边上,又矩形ABCD中,AB=1,BC=a(a>0),
∴
≥1,故a≥2,故a的取值范围[2,+∞).
∵PQ⊥QD,∴AQ⊥QD,
∴点Q在以线段AD为直径的圆上,圆的半径为
| a |
| 2 |
又点Q在BC边上,又矩形ABCD中,AB=1,BC=a(a>0),
∴
| a |
| 2 |
点评:本题体现转化的数学思想,转化为以AD为直径的圆与边BC有交点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,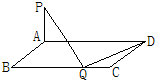 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于