题目内容
已知数列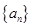 中的相邻两项
中的相邻两项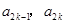 是关于
是关于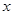 的方程
的方程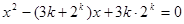 的两个根,且
的两个根,且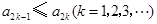 .
.
(I)求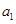 ,
,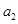 ,
,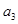 ,
,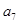 ;
;
(II)求数列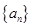 的前
的前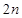 项和
项和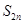 ;
;
(Ⅲ)记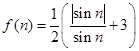 ,
,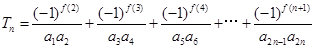 ,
,
求证: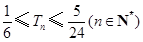 .
.
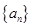 中的相邻两项
中的相邻两项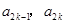 是关于
是关于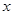 的方程
的方程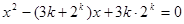 的两个根,且
的两个根,且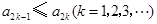 .
.(I)求
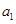 ,
,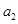 ,
,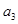 ,
,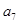 ;
; (II)求数列
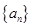 的前
的前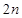 项和
项和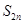 ;
;(Ⅲ)记
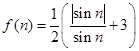 ,
,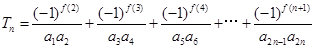 ,
,求证:
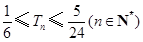 .
.(I)当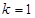 时,
时,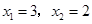 , 所以
, 所以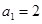 ;
;
当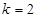 时,
时, ,
,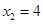 ,所以
,所以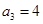 ;
;
当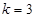 时,
时,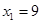 ,
,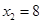 ,所以
,所以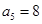 时;
时;
当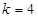 时,
时,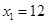 ,
,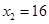 ,所以
,所以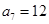 .
.
(II)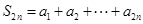
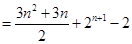 .
.
(III)证明:见解析.
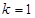 时,
时,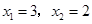 , 所以
, 所以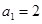 ;
;当
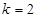 时,
时, ,
,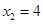 ,所以
,所以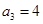 ;
;当
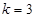 时,
时,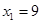 ,
,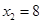 ,所以
,所以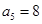 时;
时;当
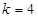 时,
时,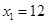 ,
,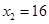 ,所以
,所以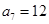 .
.(II)
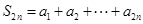
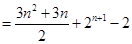 .
.(III)证明:见解析.
。本题主要考查等差、等比数列的基本知识,考查运算及推理能力.本题属难题,一般要求做(1),(2)即可,让学生掌握常见方法,对(3)不做要求.
(1)用解方程或根与系数的关系表示a2k-1,a2k,k赋值即可.
(2)由S2n=(a1+a2)+…+(a2n-1+a2n)可分组求和.
(3)Tn复杂,常用放缩法,但较难.
(I)解:方程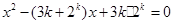 的两个根为
的两个根为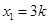 ,
,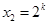 ,
,
当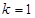 时,
时,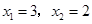 , 所以
, 所以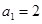 ;
;
当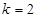 时,
时, ,
,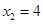 ,所以
,所以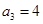 ;
;
当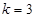 时,
时,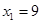 ,
,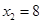 ,所以
,所以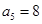 时;
时;
当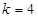 时,
时,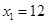 ,
,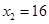 ,所以
,所以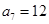 .
.
(II)解: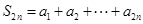
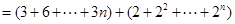
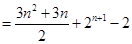 .
.
(III)证明: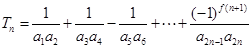 ,所以
,所以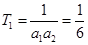 ,
,
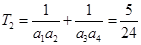 .
.
当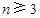 时,
时,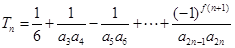 ,
,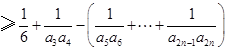

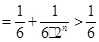 ,
,
同时,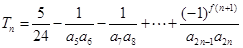
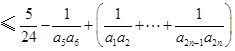
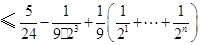
 .综上,当
.综上,当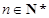 时,
时,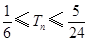 .
.
(1)用解方程或根与系数的关系表示a2k-1,a2k,k赋值即可.
(2)由S2n=(a1+a2)+…+(a2n-1+a2n)可分组求和.
(3)Tn复杂,常用放缩法,但较难.
(I)解:方程
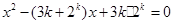 的两个根为
的两个根为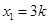 ,
,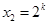 ,
,当
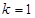 时,
时,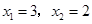 , 所以
, 所以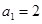 ;
;当
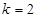 时,
时, ,
,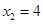 ,所以
,所以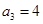 ;
;当
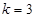 时,
时,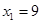 ,
,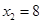 ,所以
,所以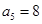 时;
时;当
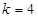 时,
时,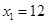 ,
,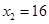 ,所以
,所以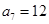 .
.(II)解:
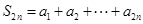
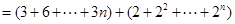
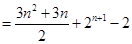 .
.(III)证明:
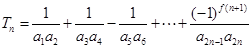 ,所以
,所以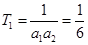 ,
,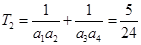 .
.当
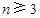 时,
时,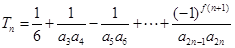 ,
,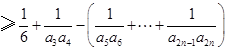

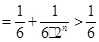 ,
,同时,
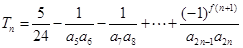
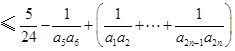
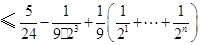
 .综上,当
.综上,当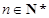 时,
时,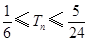 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
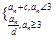
 (m是正整数),c=
(m是正整数),c=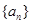 满足
满足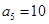 ,且
,且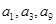 成等比数列。
成等比数列。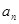 ;
;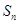 为数列
为数列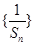 的前n项和
的前n项和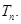
 (n∈N*),求{bn}的前n项和公式Tn.
(n∈N*),求{bn}的前n项和公式Tn.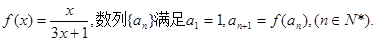
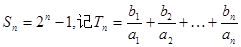 求Tn.
求Tn. 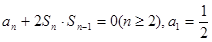
 }是等差数列;
}是等差数列; 有n条弦的长度成等差数列,最小弦长为数列的
有n条弦的长度成等差数列,最小弦长为数列的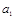 ,最大弦长为
,最大弦长为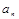 ,若公差
,若公差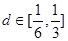 ,那么n的取值集合为( )
,那么n的取值集合为( )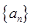 的前5项和
的前5项和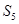 =25,且
=25,且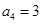 ,则
,则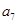 =_______
=_______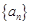 为等差数列,
为等差数列,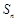 是其前n项的和,且
是其前n项的和,且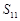 =
=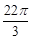 ,则
,则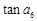 的值为
的值为