题目内容
已知定义在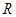 上的函数
上的函数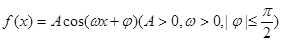 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为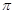 ,函数
,函数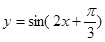 图象所有对称中心都在
图象所有对称中心都在 图象的对称轴上.
图象的对称轴上.
(1)求 的表达式;
的表达式;
(2)若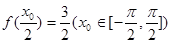 ,求
,求 的值;
的值;
(3)设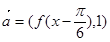 ,
,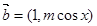 ,
, ,若
,若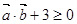 恒成立,求实数
恒成立,求实数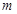 的取值范围.
的取值范围.
【答案】
(1) (2)
(2) (3)
(3)
【解析】(1)由已知中已知定义在R上的函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|≤ ),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数
),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数 图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;
图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;
(2)由 ,结合(1)中所求的函数解析式,可得
,结合(1)中所求的函数解析式,可得 ,
,
进而求出 的值,然后根据两角差的余弦公式,即可求出答案.
的值,然后根据两角差的余弦公式,即可求出答案.
(3)由  ,
, 恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.
恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.
解: (1)依题意可知: ,
,
 与f(x)相差
与f(x)相差 ,即相差
,即相差 ,
,
所以 或
或
 (舍),
(舍),
故 .
……………………4分
.
……………………4分
(2)因为 ,即
,即 ,
,
因为 ,又
,又 ,y=cosx在
,y=cosx在 单调递增,
单调递增,
所以 ,所以
,所以 ,
,
于是
 ………9分
………9分
(3)因为 ,
, ,
,
 ,
,
于是 ,得
,得 对于
对于 恒成立,
恒成立,
因为 ,故
,故 . ………………14分
. ………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数 的一个极值点,求
的一个极值点,求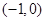 上是增函数,求实数
上是增函数,求实数 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数 上的函数
上的函数 ,则曲线
,则曲线 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.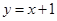 C.
C. D.
D.
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数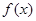 的一个极值点,求
的一个极值点,求 上是增函数,求
上是增函数,求 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 的解集为
.
的解集为
.