题目内容
已知(3x+y)2001+x2001+4x+y=0,则4x+y的值为______..
构造函数f(x)=x2001+x,则(3x+y)2001+(3x+y)+x2001+x=0
∴f(3x+y)+f(x)=0
∵f(-x)=-(x2001+x)=-f(x)且定义域为R关于原点对称
∴f(x)的奇函数
∴f(3x+y)=f(-x)
又易得f(x)=x2001+x为R上的单调递增函数
∴3x+y=-x
∴4x+y=0
故答案为0
∴f(3x+y)+f(x)=0
∵f(-x)=-(x2001+x)=-f(x)且定义域为R关于原点对称
∴f(x)的奇函数
∴f(3x+y)=f(-x)
又易得f(x)=x2001+x为R上的单调递增函数
∴3x+y=-x
∴4x+y=0
故答案为0

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知变量x,y满足约束条件
,则z=3x+y的最小值为( )
|
| A、2 | B、1 | C、-1 | D、-2 |
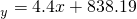 ,则可估计x与y的增长速度之比约为
,则可估计x与y的增长速度之比约为 .
. ,m)三点共线,则m的值为2.
,m)三点共线,则m的值为2.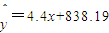 ,则可估计x与y的增长速度之比约为
,则可估计x与y的增长速度之比约为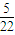 .
. ,m)三点共线,则m的值为2.
,m)三点共线,则m的值为2.