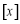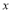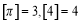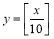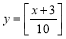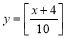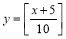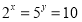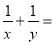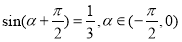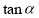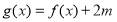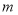题目内容
已知函数 ,且
,且 .
.
(1)判断 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断 在区间
在区间 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若在区间 上,不等式
上,不等式 恒成立,试确定实数
恒成立,试确定实数 的取值范围.
的取值范围.
(1)函数 在
在 上为奇函数;(2)函数
上为奇函数;(2)函数 在
在 上是增函数(3)实数
上是增函数(3)实数 的取值范围是
的取值范围是
【解析】
试题分析:(1)由条件 可求得函数解析式中的
可求得函数解析式中的 值,从而求出函数的解析式,求出函数的定义域并判断其是否关于原点对称(这一步很容易被忽略),再通过计算
值,从而求出函数的解析式,求出函数的定义域并判断其是否关于原点对称(这一步很容易被忽略),再通过计算 ,与
,与 进行比较解析式之间的正负,从而判断
进行比较解析式之间的正负,从而判断 的奇偶性;(2)由(1)可知函数的解析式,根据函数单调性的定义法进行判断求解,(常用的定义法步骤:取值;作差;整理;判断;结论);(3)由(1)可将函数解析式代入不等式可得
的奇偶性;(2)由(1)可知函数的解析式,根据函数单调性的定义法进行判断求解,(常用的定义法步骤:取值;作差;整理;判断;结论);(3)由(1)可将函数解析式代入不等式可得 ,经未知数与待定数分离得
,经未知数与待定数分离得 ,在区间
,在区间 上求出
上求出 的最小值,从而确定实数
的最小值,从而确定实数 的取值范围.
的取值范围.
试题解析:(1)由 得:
得: 
∴ ,其定义域为
,其定义域为 关于原点对称
关于原点对称
又
∴函数 在
在 上为奇函数。 4分
上为奇函数。 4分
(2)函数 在
在 上是增函数,证明如下:
上是增函数,证明如下:
任取 ,且
,且 ,则
,则 ,
,
那么

即 ∴函数
∴函数 在
在 上是增函数。 8分
上是增函数。 8分
(3)由 ,得
,得
 ,在区间
,在区间 上,
上, 的最小值是
的最小值是 ,
, ,得
,得 ,
,
所以实数 的取值范围是
的取值范围是 . 14分
. 14分
考点:1.函数的概念、奇偶性、单调性、最值;2.不等式.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目