题目内容
如图,在三棱锥 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)若平面 平面
平面 ,
, ,求证:
,求证: .
.
【答案】
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)这是一个证明直线和平面平行的问题,考虑直线与平面平行的判定定理,可找面外线平行于面内线,本题容易找到 ,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.
,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.
试题解析:(1)在 中,
中, 、
、 分别是
分别是 、
、 的中点,所以
的中点,所以 ,
,
又 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 . 6分
. 6分
(2)在平面 内过点
内过点 作
作 ,垂足为
,垂足为 .因为平面
.因为平面 平面
平面 ,平面
,平面 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 , 8分
, 8分
又 平面
平面 ,所以
,所以 , 10分
, 10分
又 ,
, ,
, 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 , 12分
, 12分
又 平面
平面 ,所以
,所以 . 14分
. 14分

考点:直线与平面平行的判定、直线与平面垂直的判定,平面与平面垂直的性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
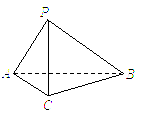 如图,在三棱锥
如图,在三棱锥









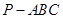 中,
中,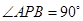 ,
,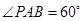 ,
,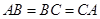 ,点
,点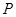 在平面
在平面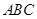 内的射影
内的射影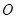 在
在 上。
上。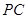 与平面
与平面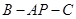 的大小。
的大小。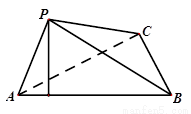
 中,已知点
中,已知点 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点.
的中点.
 ∥平面
∥平面 ;
; ,
, ,求证:
,求证: .
.