题目内容
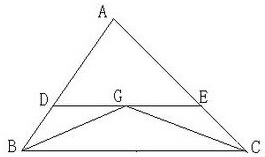
△ABC中，重心G在DE上，且DE∥BC，则
= ，
= ．
| S△ADE |
| SBCED |
| S△ABG |
| S△GBC |
考点：相似三角形的性质
专题：几何证明
分析：根据重心的性质得出
=
，再结合相似三角形的判定与性质得出
=
=
，进而得出S△ADE：S△ABC=4：9．进而得到
的值，再由S△ABG：S△ABC=1：3及S△GBC：S△ABC=1：3，得到
的值．
| AG |
| AF |
| 2 |
| 3 |
| DE |
| BC |
| AG |
| AF |
| 2 |
| 3 |
| S△ADE |
| SBCED |
| S△ABG |
| S△GBC |
解答：解：连接AG并延长交BC于一点F，
∵点G是△ABC的重心，
∴
=
，
∵DE∥BC，
∴△ADE∽△ABC，△AGE∽△AFC，△ADG∽△ABF，
∴
=
=
，
∴S△ADE：S△ABC=4：9．
∴
=
，
又由S△ABG：S△ABC=1：3．
S△GBC：S△ABC=1：3．
∴
=1，
故答案为：
，1．
∵点G是△ABC的重心，
∴
| AG |
| AF |
| 2 |
| 3 |
∵DE∥BC，
∴△ADE∽△ABC，△AGE∽△AFC，△ADG∽△ABF，
∴
| DE |
| BC |
| AG |
| AF |
| 2 |
| 3 |
∴S△ADE：S△ABC=4：9．
∴
| S△ADE |
| SBCED |
| 4 |
| 5 |
又由S△ABG：S△ABC=1：3．
S△GBC：S△ABC=1：3．
∴
| S△ABG |
| S△GBC |
故答案为：
| 4 |
| 5 |
点评：此题主要考查了相似三角形的判定与性质以及重心的知识，根据重心知识得出
=
，以及进而得出
=
=
，是解决问题的关键．
| AG |
| AF |
| 2 |
| 3 |
| DE |
| BC |
| AG |
| AF |
| 2 |
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
设复数z=
（i为虚数单位），则|z|=（ ）
| 2 |
| 1+i |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
在二项式(
+
)n的展开式中只有第五项的二项式系数最大，把展开式中所有的项重新排成一列，则有理项都互不相邻的概率为（ ）
| x |
| 2 | |||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
（1+ax+by）n展开式中不含x的项的系数的绝对值的和为32，不含y的项的系数的绝对值的和为243，则a，b，n的值可能为（ ）
| A、a=-1，b=2，n=5 | B、a=2，b=1，n=5 | C、a=2，b=-1，n=6 | D、a=-1，b=-2，n=6 |
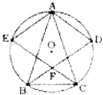如图，AB=AC，∠ABC，∠ACB的平分线BD，CE分别交△ABC的外接圆D，E，且BD、CE相交于点F，则四边形AEFD是（ ）| A、圆内接四边形 | B、菱形 | C、梯形 | D、矩形 |
已知矩阵A的逆矩阵A-1=
，则矩阵A的特征值为（ ）
|
| A、-1 | B、4 |
| C、-1，4 | D、-1，3 |