题目内容
设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若不等式
,若不等式 对区间
对区间 内任意的两个不相等的实数
内任意的两个不相等的实数 都成立,则不等式
都成立,则不等式 的解集是 。
的解集是 。

解析试题分析:∵ 对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
∴函数g(x)=xf(x)在(-∞,0)上单调递减,又 f(x)为奇函数,∴g(x)=xf(x)为偶函数,g(x)在(0,+∞)上单调递增,且g(-1)=g(1)=0,
作出g(x)的草图如图所示:
xf(2x)<0即2xf(2x)<0,g(2x)<0,
由图象得,-1<2x<0或0<2x<1,解得- <x<0或0<x<
<x<0或0<x< ,
,
∴不等式xf(2x)<0解集是 ,
,
故答案为: .
.
考点:函数的奇偶性、单调性及其应用;不等式的求解;运用函数性质化抽象不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ;
; ,则
,则 必要非充分条件;
必要非充分条件; ;
;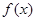 满足
满足 ,则函数图象关于直线
,则函数图象关于直线 对称.
对称. 上的奇函数
上的奇函数 满足
满足 ,若
,若 ,则实数
,则实数 的取值范围为 .
的取值范围为 .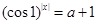 有两个根,则
有两个根,则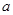 的范围为
的范围为  ,
, ,若
,若 ,对
,对 ,
, ,则
,则 。
。
 ,则
,则 .
. 的定义域为 .
的定义域为 . 的方程
的方程 在区间
在区间 上有两个不同的实数解,则实数
上有两个不同的实数解,则实数 的取值范围为 .
的取值范围为 .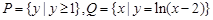 ,则
,则 = .
= .