题目内容
若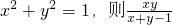 的最大值为________.
的最大值为________.
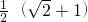
分析:法1:令f=x+y,则f2=(x+y)2≤2(x2+y2)=2,所以f≤
 .由xy=
.由xy=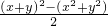 =
=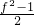 ,知
,知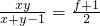 ≤
≤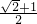 .由此能求出
.由此能求出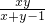 的最大值.
的最大值.法2:令x=cosa,y=sina,则 xy=cosa•sina=[(cos(
 ))2-(sin(
))2-(sin( ))2]•2sin(
))2]•2sin( )cos(
)cos( )=sin(
)=sin( )•[cos(
)•[cos( )-sin(
)-sin( )]•(1+cosa+sina),而x+y-1=sina+cosa-1=2sin(
)]•(1+cosa+sina),而x+y-1=sina+cosa-1=2sin( )cos(
)cos( )-2(sin(
)-2(sin( ))2=2sin(
))2=2sin( )•[cos(
)•[cos( )-sin(
)-sin( )],由此能求出
)],由此能求出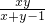 的最大值.
的最大值.解答:解法1:令f=x+y,
则f2=(x+y)2≤2(x2+y2)=2,
所以f≤
 .
.另一方面xy=
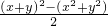 =
=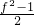 ,
,所以
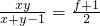 ≤
≤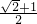 .
.当x=y=
 时,
时,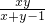 取到最大值
取到最大值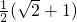 .
.解法2:令x=cosa,y=sina,
则 xy=cosa•sina=[(cos(
 ))2-(sin(
))2-(sin( ))2]•2sin(
))2]•2sin( )cos(
)cos( )
)=2sin(
 )•[cos(
)•[cos( )-sin(
)-sin( )]•[cos(
)]•[cos( )+sin(
)+sin( )]•cos(
)]•cos( )
)=sin(
 )•[cos(
)•[cos( )-sin(
)-sin( )]•(1+cosa+sina),
)]•(1+cosa+sina),而x+y-1=sina+cosa-1
=2sin(
 )cos(
)cos( )-2(sin(
)-2(sin( ))2
))2=2sin(
 )•[cos(
)•[cos( )-sin(
)-sin( )],
)],所以
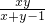 =
= (1+cosa+sina)
(1+cosa+sina)=
 (1+
(1+ sin(a+
sin(a+ ))
))≤
 (1+
(1+ ),
),所以当x=y=
 时,
时,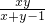 的最大值为
的最大值为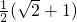 .
.点评:本题考查函数值域的求法,解题时要认真审题.,仔细挖掘题设中的隐含条件,在解法1国要注意均值不等式的合理运用,在解法2中要注意三角函数的灵活运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 设
设 若
若 ,其中
,其中 满足
满足 ,若
,若 的最大值为6,则
的最大值为6,则
 。
。 ,若
,若 的最大值为
的最大值为 ,
,
 的二次项系数为
的二次项系数为 ,且不等式
,且不等式 的解集为
的解集为 .
. 有两个相等的实数根, 求
有两个相等的实数根, 求 轴上。离心率为
轴上。离心率为 ,点
,点 是椭圆上的一个动点,
是椭圆上的一个动点, 的最大值为
的最大值为 ,求椭圆的标准方程.
,求椭圆的标准方程.