题目内容
已知函数f(x)=
cos(-π-
)sin(3π+
)-cos2
+1.
(Ⅰ)用五点作图法,作出函数f(x)在[0,2π]上的简图;
(Ⅱ)若x∈[0,
],f(x)=
,求cosx的值.
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
(Ⅰ)用五点作图法,作出函数f(x)在[0,2π]上的简图;
(Ⅱ)若x∈[0,
| π |
| 2 |
| 11 |
| 10 |
分析:(Ⅰ)将f(x)化简为f(x)=sin(x-
)+
,利用五点作图法,作出函数f(x)在[0,2π]上的简图即可;
(Ⅱ)依题意,可求得sin(x-
)=
,cos(x-
)=
,利用cosx=cos[(x-
)+
]即可求得答案.
| π |
| 6 |
| 1 |
| 2 |
(Ⅱ)依题意,可求得sin(x-
| π |
| 6 |
| 3 |
| 5 |
| π |
| 6 |
| 4 |
| 5 |
| π |
| 6 |
| π |
| 6 |
解答:解(Ⅰ)∵f(x)=-
cos
•(-sin
)-
+1
=
sinx-
cosx+
=sin(x-
)+
,
∵x∈[0,2π],列表如下:
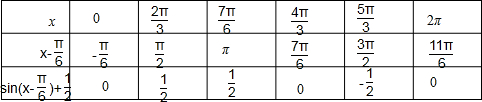
作图如下:
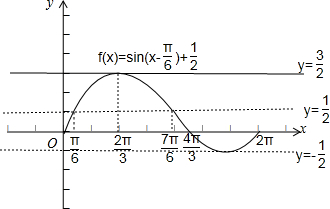
(Ⅱ)∵f(x)=sin(x-
)+
,f(x)=
,
∴sin(x-
)=
,
又x∈[0,
],
∴x-
∈[-
,
],
即cos(x-
)=
,
∴cosx=cos[(x-
)+
]
=cos(x-
)cos
-sin(x-
)sin
=
-
.
| 3 |
| x |
| 2 |
| x |
| 2 |
| 1+cosx |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(x-
| π |
| 6 |
| 1 |
| 2 |
∵x∈[0,2π],列表如下:

作图如下:

(Ⅱ)∵f(x)=sin(x-
| π |
| 6 |
| 1 |
| 2 |
| 11 |
| 10 |
∴sin(x-
| π |
| 6 |
| 3 |
| 5 |
又x∈[0,
| π |
| 2 |
∴x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
即cos(x-
| π |
| 6 |
| 4 |
| 5 |
∴cosx=cos[(x-
| π |
| 6 |
| π |
| 6 |
=cos(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
4
| ||
| 10 |
| 3 |
| 10 |
点评:本题考查五点法作函数y=Asin(ωx+φ)的图象,考查运用诱导公式化简求值与两角和的余弦,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |