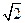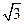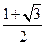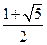题目内容
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,右准线方程为x=
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线x-y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线x-y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.
(Ⅰ)由题意,得
,解得a=1,c=
,
∴b2=c2-a2=2,
∴所求双曲线C的方程为x2-
=1.
(Ⅱ)设A、B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由
得x2-2mx-m2-2=0(判别式△>0),
∴x0=
=m,y0=x0+m=2m,
∵点M(x0,y0)在圆x2+y2=5上,
∴m2+(2m)2=5,∴m=±1.
|
| 3 |
∴b2=c2-a2=2,
∴所求双曲线C的方程为x2-
| y2 |
| 2 |
(Ⅱ)设A、B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由
|
∴x0=
| x1+x2 |
| 2 |
∵点M(x0,y0)在圆x2+y2=5上,
∴m2+(2m)2=5,∴m=±1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
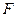 、
、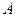 分别为双曲线
分别为双曲线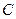 :
: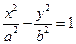
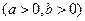 的左焦点、右顶点,点
的左焦点、右顶点,点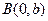 满足
满足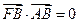 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )