题目内容
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在 处投;方案2:都在
处投;方案2:都在 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为 ,在
,在 处投篮的命中率为
处投篮的命中率为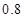 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
(Ⅰ)0.32 (Ⅱ)甲同学应选择方案2通过测试的概率更大
解析试题分析:(Ⅰ)在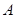 处投篮命中记作
处投篮命中记作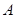 ,不中记作
,不中记作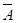 ;在
;在 处投篮命中记作
处投篮命中记作 ,不中记作
,不中记作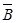 ;
;
甲同学测试结束后所得总分为4可记作事件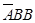 ,则
,则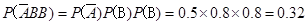
解: 的所有可能取值为
的所有可能取值为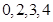 ,则
,则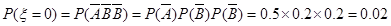
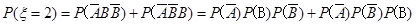
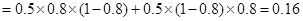
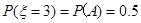
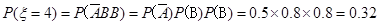
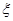 的分布列为:
的分布列为:
7分
0 2 3 4 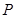
0.02 0.16 0.5 0.32 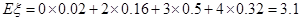 ,
,
(Ⅱ)解:甲同学选择方案1通过测试的概率为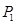 ,选择方案2通过测试的概率为
,选择方案2通过测试的概率为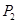 ,
, 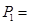
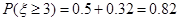

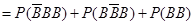 =
=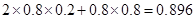
因为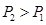
所以 甲同学应选择方案2通过测试的概率更大.
考点:古典概型及其概率计算公式;离散型随机变量的期望与方差.
点评:本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识.体现数学的科学价值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为xl,x2,x3,等级编号为5的2件产品记为yl ,y2,现从xl,x2,x3,yl,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件品的级编号恰好相同的概率。
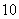 个编号为
个编号为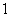 、
、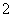 、
、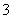 的球,
的球, 个,
个,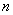 个.从袋中依次摸出
个.从袋中依次摸出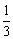 .
.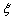 ,求随机变量
,求随机变量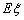 .
.
 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
, 是锐角三角形的概率。
是锐角三角形的概率。