题目内容
已知函数f(x)=
,求导函数f'(x),并确定f(x)的单调区间.
| 2x-b |
| (x-1)2 |
f′(x)=
=
=-
.
令f'(x)=0,得x=b-1.
当b-1<1,即b<2时,f'(x)的变化情况如下表:
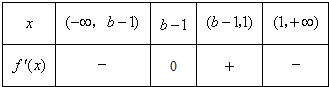
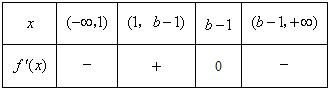
当b-1>1,即b>2时,f'(x)的变化情况如下表:
所以,当b<2时,函数f(x)在(-∞,b-1)上单调递减,在(b-1,1)上单调递增,
在(1,+∞)上单调递减.
当b>2时,函数f(x)在(-∞,1)上单调递减,在(1,b-1)上单调递增,在(b-1,+∞)上单调递减.
当b-1=1,即b=2时,f(x)=-
,所以函数f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递减.
| 2(x-1)2-(2x-b)•2(x-1) |
| (x-1)4 |
| -2x+2b-2 |
| (x-1)3 |
| 2[x-(b-1)] |
| (x-1)3 |
令f'(x)=0,得x=b-1.
当b-1<1,即b<2时,f'(x)的变化情况如下表:

当b-1>1,即b>2时,f'(x)的变化情况如下表:

所以,当b<2时,函数f(x)在(-∞,b-1)上单调递减,在(b-1,1)上单调递增,
在(1,+∞)上单调递减.
当b>2时,函数f(x)在(-∞,1)上单调递减,在(1,b-1)上单调递增,在(b-1,+∞)上单调递减.
当b-1=1,即b=2时,f(x)=-
| 2 |
| (x-1)2 |

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目