题目内容
下列命题中,真命题是( )
分析:利用三角函数值判断A的正误;二次函数的判断B的正误;利用二次函数的最小值判断C的正误;通过单位圆判断D的正误.
解答:解:sinx+cosx=
sin(x+
)≤
,所以A不正确;
因为x2-2x-1>0,x∈(3,+∞),所以B不正确;
因为x2+x+1>0,所以?x∈R,x2+x=-1不正确;
利用单位圆可知?x∈(0,
),x>sinx,成立.
故选D.
| 2 |
| π |
| 4 |
| 2 |
因为x2-2x-1>0,x∈(3,+∞),所以B不正确;
因为x2+x+1>0,所以?x∈R,x2+x=-1不正确;
利用单位圆可知?x∈(0,
| π |
| 2 |
故选D.
点评:本题考查特称命题与全称命题的判断,基本知识的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
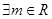 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1