题目内容
16.已知等差数列{an}的前n项和为Sn,公差d≠0,且S5=35,a1、a4、a13成等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{{a}_{n}}{{a}_{{2}^{n}-1}}$,试求数列{bn}的前n项和Tn.
分析 (I)利用等差数列与等比数列的通项公式、前n项和公式即可得出;
(II)利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(I)∵a1、a4、a13成等比数列,
∴${a}_{4}^{2}={a}_{1}•{a}_{13}$,
∴$({a}_{1}+3d)^{2}$=a1•(a1+12d),化为3d2-2a1d=0,
∵d≠0,∴3d=2a1.
∵S5=35,
∴$5{a}_{1}+\frac{5×4}{2}•d$=35,化为a1+2d=7,联立$\left\{\begin{array}{l}{3d=2{a}_{1}}\\{{a}_{1}+2d=7}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=3}\\{d=2}\end{array}\right.$.
∴an=3+2(n-1)=2n+1.
(II)设bn=$\frac{{a}_{n}}{{a}_{{2}^{n}}-1}$=$\frac{2n+1}{2×{2}^{n}+1-1}$=$\frac{2n+1}{{2}^{n+1}}$.
数列{bn}的前n项和Tn=$\frac{3}{{2}^{2}}+\frac{5}{{2}^{3}}$+$\frac{7}{{2}^{4}}$+…+$\frac{2n+1}{{2}^{n+1}}$,
$\frac{1}{2}{T}_{n}$=$\frac{3}{{2}^{3}}+\frac{5}{{2}^{4}}$+…+$\frac{2n-1}{{2}^{n+1}}$+$\frac{2n+1}{{2}^{n+1}}$,
∴$\frac{1}{2}{T}_{n}$=$\frac{3}{{2}^{2}}+\frac{2}{{2}^{3}}+\frac{2}{{2}^{4}}$+…+$\frac{2}{{2}^{n+1}}$-$\frac{2n+1}{{2}^{n+1}}$,
化为Tn=$\frac{1}{2}+1+\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{2n+1}{{2}^{n}}$=$\frac{1}{2}+\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{2n+1}{{2}^{n}}$=$\frac{3}{2}-\frac{2n+3}{{2}^{n}}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

| A. | (-∞,2) | B. | [-2,2] | C. | (-2,2) | D. | [-2,2) |
 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
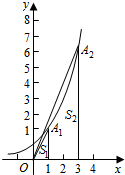
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.