题目内容
已知定义域为R的函数 是奇函数.
是奇函数.
(1)求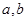 的值;
的值;
(2)证明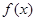 在
在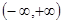
 上为减函数.
上为减函数.
(3)若对于任意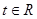 ,不等式
,不等式 恒成立,求
恒成立,求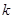 的范围.
的范围.
【答案】
(1) ; (2)见解析;
(3)
; (2)见解析;
(3)
【解析】(1)f(0)=0可得b=1,由f(-x)+f(x)=0恒成立,可得a=1.
(2) 任取 ,利用函数单调性的定义判断
,利用函数单调性的定义判断 的符合即可判断单调性.
的符合即可判断单调性.
(3)不等式 恒成立,
恒成立,
可得 ,然后利用单调性去年法则符号f,
,然后利用单调性去年法则符号f,
从而转化为 ,然后进一步转化为
,然后进一步转化为 恒成立问题来解决.
恒成立问题来解决.
(1)
 经检验
经检验 符合题意.
符合题意.
(2)任取
则
=

(3)
 ,不等式
,不等式 恒成立,
恒成立, 
 为奇函数,
为奇函数, 
 为减函数,
为减函数, 
即 恒成立,而
恒成立,而


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目